One often overlooked, but absolutely key point to understand about the lambda CDM model is that it doesn't really meaningfully specify much about the CDM part. It establishes that there must be a certain amount of very generally described non-hot dark matter, but very little more.
While just about any good model of dark matter that worked at galactic scales would also fit the lambda CDM parameters in the universe and CBM oberservations as a whole, a great many dark matter models that meet those flimsy criteria do not make good galactric or galactic cluster scale models.
The CDM that the lambda CDM models are talking about, and the CDM models that replicate other evidence of dark matter, are only vaguely related to each other and proof of one does not itself entail proof of the others.
All that lambda-CDM says about it is that cold dark matter "is described as being cold (i.e. its velocity is non-relativistic [far below the speed of light] at the epoch of radiation-matter equality), non-baryonic (consisting of matter other than protons and neutrons), dissipationless (cannot cool by radiating photons) and collisionless (i.e., the dark matter particles interact with each other and other particles only through gravity and possibly the weak force). The dark matter component is currently estimated to constitute about 23% of the mass-energy density of the universe."
Indeed, the non-baryonic assumption is actually redundant. It is implied by the Standard Model, the "cold" requirement that rules out neutrinos, and the "dissipationless" and "collisionless" requirements that rules out protons and neutrons. Basically, CDM is assumed to behave like either fertile or sterile neutrinos in their interactions but to be heavier than the single digit eV mass scale. Otherwise, the six parameter model says almost nothing about it qualitatively, even though we know that a vast part of the parameter space consistent with those characteristics have been ruled out by other means.
No candidate CDM particle and no CDM model that is an excellent fit to both sub-CMB data and the CBM data has been devised to date and the link between the source of CMB structure and phenomena like galactric rotation curves is currently only conjectural, although getting a model that works at a more localized level to generalize up in scale, in general, is quite a bit easier than a top down fit.
Backgrond on the six parameter plus model
In the lambda CDM model, the six parameters are (1) physical baryon density, (2) physical dark matter density, (3) dark energy density, (4) scalar spectral index, (5) curvature fluctuation amplitude and (6) reionization optical depth. . . . "other possible parameters are fixed at "natural" values e.g. total density = 1.00, dark energy equation of state = -1, neutrino masses are small enough to be negligible."
The fact that six paramters are all it takes to describe CMB structure is important. It rules out a whole lot of complex models and tightly constrains those that aren't ruled out to look quite similar to each other. It is a profound truth that the universe as a whole isn't terribly complicated (echoing other finds in astronomy past and present).
Of course, it may take more parameters to be prefectly accurate, but the key point is that half a dozen parameters matter much more than eveything else.
It is important in the same way that the ability of the MOND model can reproduce galactric rotation curves relative to luminous matter (and hence the quantity of and distributions of dark matter in CDM or warm dark matter (WDM) paradigms) for almost all galaxies with just one parameter. If any phenomenological model can do that then the underlying phenomena has to be a well constrained simply one even if the implicit theory in MOND of gravity modification is wrong.
Definitions of six parameters
The "physical baryon density" Ωbh2 differs from the "baryon density" Ωb in that the baryon density gives the fraction of the critical density made up of baryons (the critical density is the total density of matter/energy needed for the universe to be spatially flat, with measurements indicating that the actual total density Ωtot is very close if not equal to this value, see below), while the physical baryon density is equal to the baryon density multiplied by the square of the reduced Hubble constant h, where h is related to the Hubble constant H0 by the equation H0 = 100 h (km/s)/Mpc. Likewise for the difference between "physical dark matter density" and "dark matter density".
Dark energy is largely a massaged version of the Hubble constant that fits the cosmological constant of General Relativity scaled so that it is expressed in terms comparable to its contribution to total mass-energy in a universe that is spatially flat at a large global scale (even through there are localized curvatures in space-time).
The scalar spectral index starts with a scale invariant power law distribution of CMB hot spots and cold spots as a baseline, and then tweaks the power law to allow for a power law distribution of these hot spots and cold spots with a value other than the scale invariant unity value.
Reionization optical depth is essentially a red shift estimate of the time that the CMB formed.
Definitions of extra parameters
Additional parameters which have experimentally measured values consistent with zero include:
* Physical neutrino density, the effective number of kinds of relativistic particles as of CMB formation (basically 1 eV or less of mass) the only known forms of which are neutrinos of which there are three kinds, and the sum of the masses of the relativistic particle types, which give rise to a physical neutrino density comparable to those for baryonic matter, dark matter and dark energy. More accurately, this is a "hot dark matter" proportion parameter.
Astronomy data bound this to a negligible proportion of the total that is consistent with zero with a best fit value that is a close fit to thee neutrinos with masses in a normal hierarchy an a negligible electron neutrino mass relative to the other neutrino masses and no other relativistic species of particles. Particle physics data virtually insure that this factor, while tiny, is non-zero.
* A parameter for the possibility that the universe is not flat (based upon the sum of mass-energy component proportions (i.e. baryonic, cold dark matter, hot dark matter, dark energy).
The best fit data is with the data is about 0.2% different from flat and consistent with flat at the 0.5 sigma level.
* The equation of state of dark energy (w). A value of -1 is indistinguishable from the cosmological constant of General Relativity that determines the long term fate of the universe (expansion, contraction, etc.). A value of other than -1 would be a beyond general relativity quintessence theory that cannot be fully explained with a cosmological constant.
The equation of state may be used in Friedmann-Lemaître-Robertson-Walker equations to describe the evolution of an isotropic universe filled with a perfect fluid. Ifis the scale factor then
The equation of state of ordinary non-relativistic matter (e.g. cold dust) is, which means that it is diluted as
, where
is the volume. This means that the energy density red-shifts as the volume, which is natural for ordinary non-relativistic matter. . . .
The equation of state of ultra-relativistic matter (e.g. radiation, but also matter in the very early universe) iswhich means that it is diluted as
. In an expanding universe, the energy density decreases more quickly than the volume expansion, because radiation has momentum and, by the de Broglie hypothesis a wavelength, which is red-shifted. . . .
Cosmic inflation and the accelerated expansion of the universe can be characterized by the equation of state of dark energy. In the simplest case, the equation of state of the cosmological constant is. In this case, the above expression for the scale factor is not valid and
, where the constant H is the Hubble parameter. More generally, the expansion of the universe is accelerating for any equation of state
. The accelerated expansion of the Universe was indeed observed. According to observations, the value of equation of state of cosmological constant is near -1. Hypothetical phantom energy would have an equation of state
, and would cause a Big Rip. Using the existing data, it is still impossible to distinguish between phantom
and non-phantom
.
A freeThe best fit to the data is about -0.98 and consistent with zero at the 0.5 sigma level. A deviation would be contrary to the Standard Model-General Relativity consensus, so a deviation lacks a strong theoretical basis.scalar field [ed. i.e. a perfect fluid] has
, and one with vanishing kinetic energy is equivalent to a cosmological constant:
. Any equation of state in between, but not crossing the
barrier known as the Phantom Divide Line (PDL), is achievable, which makes scalar fields useful models for many phenomena in cosmology.
* The running of the spectral index over time (i.e. if scale dependent effects in CMB were different in the early universe than in the later universe and evolved gradually over time).
The best fit data is slightly negative but consistent with zero at about the 1.0 sigma level and neither General Relativity nor the Standard Model strongly constrain it.
* The tensor-scalar ratio (r), which measures the influence on CMB due to gravity waves during inflation relative to the influence of a simple scalar field inflaton during inflation. A detectable tensor mode would manifest as a pattern of hot and cold spots in the CMB that is a best fit to having existed despite the homogenization of inflation that would form a baseline from which later CMB patterns would emerge at a scale consistent with gravitational waves in the inflaton.
The best fit value is less than 0.24 and consistent with zero, implying that at least 99.76%+ of the observed data can be accounted for while ignoring gravity waves. This is a domain in which General Relativity as a classical rather than quantum theory can provide little guidance. Many theories of inflation are ruled out by the current value. Some very low value is expected since gravity waves are strongly predicted and probably observed, but the running of gravity with extreme GUT scale energies is not known.
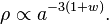
No comments:
Post a Comment