This result uses the entire dataset collected from the Tevatron collider at Fermilab. It is based on the observation of 4.2 million W boson candidates, about four times the number used in the analysis the collaboration published in 2012.
91,192.0 ± 6.4 stat ± 4.0 syst MeV [ed. combined error 7.5 MeV] (stat, statistical uncertainty; syst, systematic uncertainty), which is consistent with the world average of 91,187.6 ± 2.1 MeV.
The main problem . . . is that the new measurement is in disagreement with all other available measurements. I think this could have been presented better in their paper, mainly because the measurements of the LEP experiments have not been combined, secondly because they don't show the latest result from LHCb. Hence I created a new plot (below), which allows for a more fair judgement of the situation. I also made a back-of-envelope combination of all measurements except of CDF, yielding a value of 80371 ± 14 MeV. It should be pointed out that all these combined measurements rely partly on different methodologies as well as partly on different model uncertainties. The likelihood of the consistency of such a (simple) combination is 0.93. Depending (a bit) on the correlations you assume, this value has a discrepancy of about 4 sigma to the CDF value.In fact, there are certainly some aspects of the measurement which need to be discussed in more detail (Sorry, now follow some technical aspects, which most likely only people from the field can fully understand): In the context of the LHC Electroweak Working Group, there are ongoing efforts to correctly combine all measurements of the W boson mass; in contrast to what I did above, this is in fact also a complicated business, if you want to do it really statistically sound. My colleague and friend Maarten Boonekamp pointed out in a recent presentation, that the Resbos generator (which was used by CDF) has potentially some problems when describing the spin-correlations in the W boson production in hadron collisions. In fact, there are remarkable changes in the predicted relevant spectra between the Resbos program and the new version of the program Resbos2 (and other generators) as seen in the plot below. On first sight, the differences might be small, but you should keep in mind, that these distributions are super sensitive to the W boson mass. I also attached a small PR plot from our last paper, which indicates the changes in those distributions when we change the W boson mass by 50 MeV, i.e. more than ten times than the uncertainty which is stated by CDF. I really don't want to say that this effect was not yet considered by CDF - most likely it was already fixed since my colleagues from CDF are very experienced physicists, who know what they do and it was just not detailed in the paper. I just want to make clear that there are many things to be discussed now within the community to investigate the cause of the tension between measurements.
Difference in the transverse mass spectrum between Resbos and Resbos2 (left); impact of different W boson mass values on the shapes of transverse mass.And this brings me to another point, which I consider crucial: I must admit that I am quite disappointed that it was directly submitted to a journal, before uploading the results on a preprint server. We live in 2022 and I think it is by now good practice to do so, simply because the community could discuss these results beforehand - this allows a scientific scrutiny from many scientists which are directly working on similar topics.
More commentary from Matt Strassler is available at his blog (also here). The money quote is this one (emphasis in the original, paragraph breaks inserted editorially for ease of reading):
A natural and persistent question has been:
“How likely do you think it is that this W boson mass result is wrong?”
Obviously I can’t put a number on it, but I’d say the chance that it’s wrong is substantial.
Why?
This measurement, which took several many years of work, is probably among the most difficult ever performed in particle physics. Only first-rate physicists with complete dedication to the task could attempt it, carry it out, convince their many colleagues on the CDF experiment that they’d done it right, and get it through external peer review into Science magazine. But even first-rate physicists can get a measurement like this one wrong. The tiniest of subtle mistakes will undo it.
Physicist Tommaso Dorigo chimes in at his blog and he is firmly in the camp of measurement error and identifies some particularly notable technical issues that could cause the CDF number to be too high.
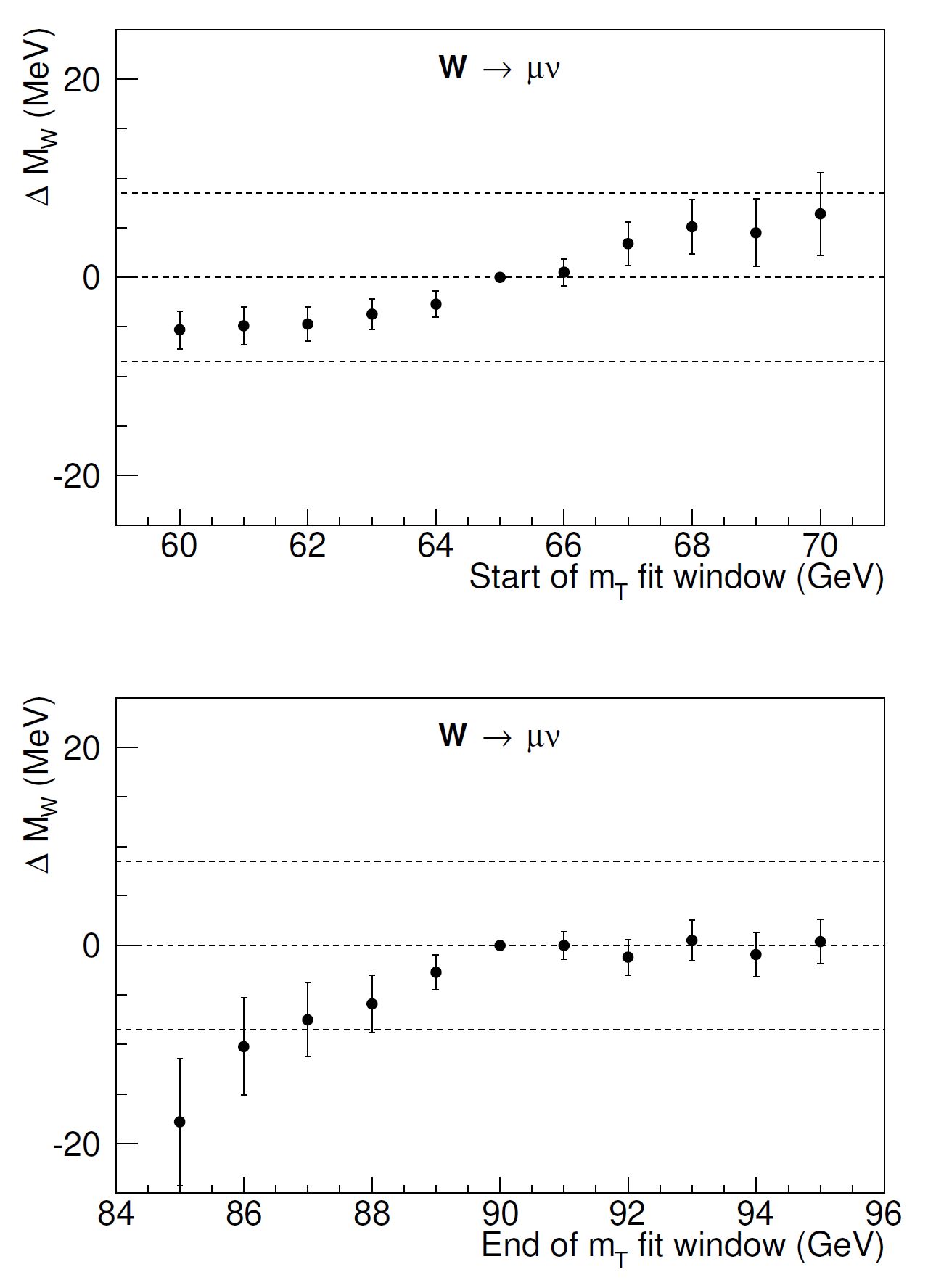
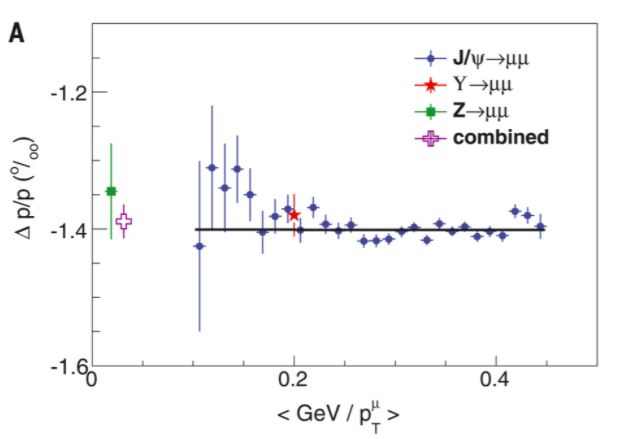
I already answered the question of whether in my opinion the new CDF measurement of the W boson mass, standing at seven standard deviations away from the predictions of the Standard Model, is a nail in the SM coffin. Now I will elaborate a little on part of the reasons why I have that conviction. I cannot completely spill my guts on the topic here though, as it would take too long - the discussion involves a number of factors that are heterogeneous and distant from the measurement we are discussing. Instead, let us look at the CDF result.One thing I noticed is that the result with muons is higher than the result with electrons. This may be a fluctuation, of course (the two results are compatible within quoted uncertainties), but if for one second we neglected the muon result, we would get a much better agreement with theory: the electron W mass is measured to 80424.6+-13.2 MeV, which is some 4.5 sigmaish away from theory prediction of 80357+-6 MeV. Still quite a significant departure, but not yet an effect of unheard-of size for accidentals.Then, another thing I notice is that CDF relied on a custom simulation for much of the phenomena involving the interaction of electrons and muons with the detector. That by itself is great work, but one wonders why not using the good old GEANT4 that all of us know and love for that purpose. It's not like they needed a fast simulation - they had the time!A third thing I notice is that the knowledge of backgrounds accounts for a significant systematic effect - it is estimated in the paper as accounting for a potential shift of two to four MeV (but is that sampled from a Gaussian distribution or can there be fatter tails?). In fact, there is one nasty background that arises in the data when you have a decay of a Z to a pair of muons, and one muon gets lost for some reconstruction issue or by failing some quality criteria. The event, in that case, appears to be a genuine W boson decay: you see a muon, and the lack of a second leg causes an imbalance in transverse momentum that can be interpreted as the neutrino from W decay. This "one-legged-Z" background is of course accounted for in the analysis, but if it had been underestimated by even only a little bit, this would drive the W mass estimate up, as the Z has a mass larger than the W (so its muons are more energetic).Connected to that note is the fact that CDF does show how their result can potentially shift significantly in the muon channel if they change the range of fitted transverse masses - something which you would indeed observe if you had underestimated the one-legged Z's in your data. This is shown in the two graphs below, where you see that the fitted result moves down by quite a few MeV if you change the upper and lower boundaries:A fourth thing I notice is that the precision of the momentum scale determination, driven by studies of low-energy resonances (J/psi and Upsilon decays to muon pairs) is outstanding, but the graph that CDF shows to demonstrate it is a bit suspicious to my eyes - it is supposed to demonstrate a flat response as a function of inverse momentum, but to my eyes it in fact shows the opposite. Here is what I am talking about:
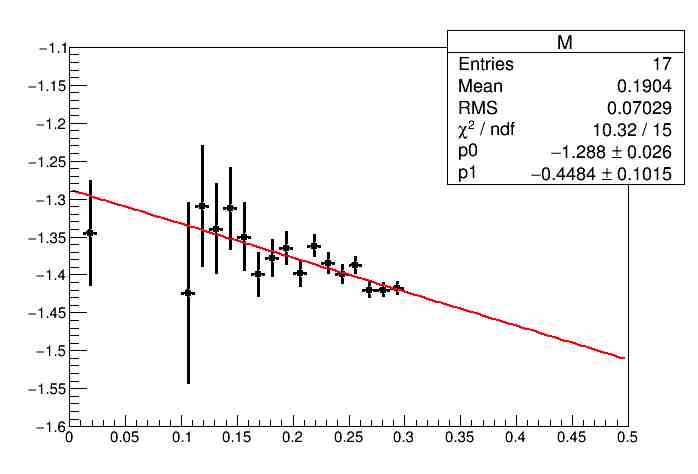
I took the liberty to take those data points and fit them with a different assumption - not a constant, but a linear slope, and not the full spectrum, but only up to inverse momenta of 0.3; and here is what I get:Of course, nobody knows what the true model of the fitting function should be; but a Fisher F test would certainly prefer my slope fit to a constant fit. Yes, I have neglected the points above 0.3, but who on earth can tell me that all these points should line up in the same slope? So, what I conclude from my childish exercise is that the CDF calibration data points are not incompatible (but IMHO better compatible) with a slope of (-0.45+-0.1)*10^-3 GeV.What that may mean, given that they take the calibration to be -1.4 from a constant fit, is to get the scale wrong by about a part in ten thousand at the momentum values of relevance for the W mass measurement in the muon channel. This is an effect of about 8 MeV, which I do not see accounted for in the list of systematics that CDF produced. [One caveat is that I have no idea whether the data points have correlated uncertainties among the uncertainty bars shown, which would invalidate my quick-and-dirty fit result.]I could go on with other things I notice, and you clearly see we would not gain much. My assessment is that while this is a tremendously precise result, it is also tremendously ambitious. Taming systematic uncertainties down to effects of a part in ten thousand or less, for a subnuclear physics measurement, is a bit too much for my taste. What I am trying to say is that while we understand a great deal about elementary particles and their interaction with our detection apparatus, there is still a whole lot we don't fully understand, and many things we are assuming when we extract our measurements. . . .
I can also say that the CDF measurement is slamming a glove of challenge on ATLAS and CMS faces. Why, they are sitting on over 20 times as much data as CDF was able to analyze, and have detectors built with a technology that is 20 years more advanced than that of CDF - and their W mass measurements are either over two times less precise (!!, the case of ATLAS), or still missing in action (CMS)? I can't tell for sure, but I bet there are heated discussions going on at the upper floors of those experiments as we speak, because this is too big a spoonful of humble pie to take on.
He also reminds us of the fact that real world uncertainties don't have a Gaussian (i.e. "normal") distribution and instead have "fat tails" with extreme deviations from expected values being more common than expected in a Gaussian distribution.
Likewise physicist Sabine Hossenfelder tweets:
Could this mean the standard model is wrong? Yes. But more likely it's a problem with their data analysis. Fwiw, I don't think this is a case for theorists at all. Theorists will explain whatever data you throw at them.
Footnote Regarding Definitional Issues




9 comments:
A systemic uncertainty of 19.7 MeV for the new CDF result and a combined uncertainty of 20.7 MeV for the new CDF result would make this is roughly 90th percentile outlier experimentally (as it should be as the outlier of 11 data points) and perhaps 3.1 sigma or so from global electroweak fit (which isn't far from the mark for a one in 11 data point fit).
Thus, if 12.8 MeV of systemic uncertainty is overlooked in the paper, you get a result that makes sense. Overlooking sources of systemic uncertainty with this combined uncertainty is very easy to do.
A new post from Jester notes that the Particle Data Group does in situations like this is to basically what I did in my previous comment (i.e. to inflate error bars to a point where the results can be reconciled, but unlike me, inflating all error bars of all experiments proportionately). http://resonaances.blogspot.com/2022/04/how-large-is-w-boson-anomaly.html
"Applying this procedure to the W mass measurements, it is necessary to inflate the errors by the factor of S=2.1, which leads mW = 80.410(15) GeV."
This is a tension with the global electroweak fit, but three sigma instead of seven sigma.
Jester also notes in the same post:
"The tension between CDF and the combination of the remaining mW measurements is whopping 4.1 sigma. What value of mW should we then use in the Standard Model fits and new physics analyses? Certainly not the CDF one, some 6.5 away from the Standard Model prediction, because that value does not take into account the input from other experiments. At the same time we cannot just ignore CDF. In the end we do not know for sure who is right and who is wrong here. While most physicists tacitly assume that CDF has made a mistake, it is also conceivable that the other experiments have been suffering from the confirmation bias. Finally, a naive combination of all the results is not a sensible option either. Indeed, at face value the Gaussian combination leads to mW = 80.410(7) GeV. This value is however not very meaningful from the statistical perspective: it's impossible to state, with 68 percent confidence, that the true value of the W mass is between 80.403 and 80.417 GeV. That range doesn't even overlap with either of the most precise measurements from CDF and ATLAS! . . . Due to the disagreement between the experiments, our knowledge of the true value of mW is degraded, and the combination should somehow account for that.
The question of combining information from incompatible measurements is a delicate one, residing at a boundary between statistics, psychology, and arts. Contradictory results are rare in collider physics, because of a small number of experiments and a high level of scrutiny. However, they are common in other branches of physics, just to mention the neutron lifetime or the electron g-2 as recent examples. To deal with such unpleasantness, Particle Data Group developed a totally ad hoc but very useful procedure. The idea is to penalize everyone in a democratic way, assuming that all experimental errors have been underestimated. More quantitatively, one inflates the errors of all the involved results until the χ^2 per degree of freedom in the combination is equal to 1."
I added this comment to his post which I think makes more sense than treating a global electroweak fit as a "Standard Model prediction":
"Is there something to be said for incorporating a global electroweak fit that doesn't include any of the mW measurements as as one additional low uncertainty "indirect measurement" in computing a global average value, rather than using it as a set of goalposts with which to judge the other experimental measurements?"
Woit says:
"There has been a lot of coverage in the press of claims by a group analyzing old CDF data to have come up with a dramatically better value for the W mass (one seven sigma away from the SM value). While this would be really wonderful if it were true, unfortunately that doesn’t seem very likely. There isn’t a well-motivated theoretical reason for this discrepancy, this is a very challenging measurement, and the new value seriously disagrees with several previous measurements at CERN. For an informed discussion of this from someone who was on CDF and has worked on these sorts of analyses, see Tommaso Dorigo’s blog post." https://www.math.columbia.edu/~woit/wordpress/?p=12775
A powerpoint look at the error estimation by the latest CDF result (probably too low). https://indico.cern.ch/event/1108518/contributions/4691380/attachments/2392473/4090175/combi_160222_EWWG.pdf
Commentary from 4gravitons:
https://4gravitons.com/2022/04/22/w-is-for-why/
"This result shakes my faith in that a little. Probably, the analysis team got something wrong. Possibly, all previous analyses got something wrong. Either way, a lot of very careful smart people tried to estimate their precision, got very confident…and got it wrong. . . .
If some future analysis digs down deep in precision, and finds another deviation from the Standard Model, should we trust it? What if it’s measuring something new, and we don’t have the prior experiments to compare to? . . .
Statistics are supposed to tell us whether to trust a result. Here, they’re not doing their job. And that creates the scary possibility that some anomaly shows up, some real deviation deep in the sigmas that hints at a whole new path for the field…and we just end up bickering about who screwed it up. Or the equally scary possibility that we find a seven-sigma signal of some amazing new physics, build decades of new theories on it…and it isn’t actually real.
We don’t just trust statistics. We also trust the things normal people trust. Do other teams find the same result? (I hope that they’re trying to get to this same precision here, and see what went wrong!) Does the result match other experiments? Does it make predictions, which then get tested in future experiments?"
More from Matt Strassler discussing some BSM options.
https://profmattstrassler.com/2022/04/13/the-simplest-way-to-shift-the-w-boson-mass/
and his first post on the topic that I didn't notice before:
https://profmattstrassler.com/2022/04/07/the-w-boson-isnt-behaving/
A new post from Sabine Hossenfelder:
http://backreaction.blogspot.com/2022/04/did-w-boson-just-break-standard-model.html
"Is it correct? I don’t know. It could be. But in all honesty, I am very skeptical that this result will hold up. More likely, they have underestimated the error and their result is actually compatible with the other measurements."
Post a Comment