Strong Force Coupling Constant Measured In Tau Decays

This measurement of the strong force coupling constant of 0.1171(10) when the measurement is converted to the W boson mass scale is just 0.6 sigma away from the Particle Data Group value of 0.1179(9) at the W boson mass scale (combining the uncertainties in quadrature). About two-thirds of the uncertainty in the latest measurement is statistical, so there is room to improve the precision of this measurement with mere brute force additional data collection.

It is also solid evidence of the soundness of the Standard Model prediction for the running of the strong force coupling constant with energy scale, which is established in the Standard Model by a beta function that is determined exactly from theory.

And, this is a good reminder that the strength of the strong force coupling constant is much stronger, 0.3077(75), at the tau lepton mass of about 1,776.86(12) MeV, which is much closer to the typical hadronic energy scale, than it is at the usually quoted value at the W boson mass of 80,379(12) MeV. 

The strong force coupling constant gets even larger at smaller masses. The peak value of the strong force coupling constant, of almost 1.0000, is at an energy scale at or below the proton mass, after which is declines, although there is dispute over whether it declines to zero or to a fixed value more than zero.

The high precision of this physical constant extraction from experimental data was made possible largely by improvements in the formulas used to do so. Using the decays of a fundamental lepton, whose mass and properties are known very precisely, into familiar and well understood pions and kaons, also helps the precision of the measurement.

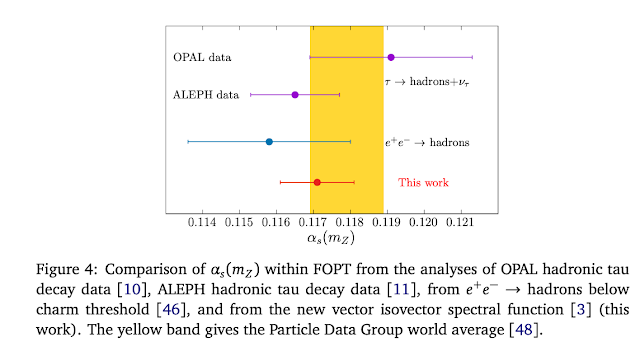
We perform a precise extraction of the QCD coupling at the τ-mass scale, α(s)(m(τ)), from a new vector isovector spectral function which combines ALEPH and OPAL distributions for the dominant channels, τ→ππ(0)ν(τ), τ→3ππ(0)ν(τ) and τ→π3π(0)ν(τ), with estimates of sub-leading contributions obtained from electroproduction cross-sections using CVC, as well as BaBar results for τ→K(−)K(0)ν(τ.) The fully inclusive spectral function thus obtained is entirely based on experimental data, without Monte Carlo input. 

From this new data set, we obtain α(s)(m(τ))=0.3077±0.0075, which corresponds to α(s)(m(Z))=0.1171±0.0010. 

This analysis can be improved on the experimental side with new measurements of the dominant ππ0, π3π0, and 3ππ0 τ decay modes.

Diogo Boito, et al., "Strong coupling at the τ-mass scale from an improved vector isovector spectral function" arXiv:2112.05413 (December 10, 2021) (Contribution to the Proceedings of "The 16th International Workshop on Tau Lepton Physics (TAU2021) (Virtual Edition)", from September 27th to October 1st 2021, Indiana University).