Why is so much attention devoted to Supersymmetry (SUSY) theories?
Supersymmetry theories include the Standard Model particles, at least one superpartner particle for each of the Standard Model particles (a fermion for each boson and a boson for each fermion), and also have multiple Higgs bosons, some charged and some electromagnetically neutral - generally at least five in all, rather than the one of the Standard Model. This resolved theoretical issues with the high energy behavior of the Standard Model equations and also provided more structure to the relationship of different constants in the theory.
In particular, it solved the "hierarchy problem." The hierarchy problem involves the question of how all of the huge valued terms in the formula for determining the Higgs boson mass in the Standard Model manage to balance out to 125 GeV give or take. Each fermion that interacts with the Higgs boson makes a positive contribution to the value, while each boson that interacts with the Higgs boson makes a negative contribution to the value. The total value is particularly sensitive to the most massive particles in existence. There is no mathematically transparent way yet known to show how all of the many terms that go into this calculation manage to come so close to cancelling out, and yet have a non-zero total. The organizing principle behind SUSY was to put together a set of particles such that the math necessary to show that these terms cancelled out to give a low Higgs boson mass was obvious and natural. Without these cancellations, very massive beyond the Standard Model particles that interact with the Higgs boson would be impossible, and SUSY's original designers thought that there were probably more particles out there to be discovered.
SUSY also caused the running coupling constants of the three Standard Model forces (electromagnetic, weak nuclear and strong nuclear) to naturally converge at a single force strength at a particular energy, something that doesn't happen with the Standard Model beta functions that govern the running of the coupling constants, although it would not be particularly difficult to simply modify the beta functions without creating a riot of new particles to achieve this end.
Essentially all versions of String Theory have a SUSY theory as one component of the overall theoretical structure. The few stable particles in SUSY theories offer attractive dark matter candidates that are absent in the Standard Model.
As Not Even Wrong commentator Bob Jones, discussing a recent talk by Nima Arkani-Hamed who spoke on The Inevitability of Physical Laws: Why the Higgs Has to Exist explained:
[Nima Arkani-Hamed] was saying that there are theoretical reasons why we can only discover elementary particles having spins 0, 1/2, 1, 3/2, and 2, and SUSY is required for spin 3/2. So because of theoretical constraints, SUSY is one of the very general ways in which new physics can show up in particle accelerators, and that’s why people are looking for it. In Arkani-Hamed’s own words,“The reason why there is so much excitement about supersymmetry is—it doesn’t mean that it has to be right—it’s the last remaining thing. It’s the last thing that nature could do, in principle, that we haven’t seen it do. And we saw something fairly dramatic with the Higgs already. We saw the zero option used, so it’s not crazy that it’s going to come along with the whole thing, we’ll finally see the whole panoply actually used in the way nature works.”
Superpartners of Standard Model particles and extra Higgs bosons in supersymmetry theories are assumed to be heavy (and mostly too heavy to detect with sub-TeV energy scale experiments), and except for one or two of them, they are unstable. The basic structure of SUSY models in terms of quantum mechanical behavior of particular particles interacting with each other is also essentially identical to that of the Standard Model with the exception of a few of the "moving parts" of the model. So, the Standard Model is an effective theory that is equivalent to SUSY at low energies in many respects. But, SUSY has subtly different expected high energy behavior than the Standard Model that ought to be possible to detect, at least in theory, and it is more complex than the Standard Model and hence to be disfavored to the extent that it is indistinguishable from it via observations.
The Experimental Vise Of SUSY Bounds
The minimum mass scale of supersymmetric particles has been pushed high enough by experimental exclusions of the large hadron collider of lighter possible supersymmetric particle mass.
Meanwhile, an experimental upper limit of the mass scale of the parameters of SUSY theories that flows from the non-detection of neutrinoless double beta decay at the higher rates predicted in SUSY theories with heavier supersymmetric particles, and by a determination of the Higgs boson mass.
This vise of experimental constraints on supersymmetric particle masses from below and above has already falsified more plain vanilla versions of supersymmetry theories. This vise also dramatically shrinks the parameter space of SUSY theories that hasn't been ruled out by the LHC because the LHC can't reach or has not yet reached such high energies.
Other new experimental constraints on SUSY models are also beginning to have an impact on SUSY parameter space.
Higgs Boson Mass Constraints On SUSY Models
It is also worth recalling, as I have noted previously, that:
[O]ne of the effects of finding a "lightest Higgs boson mass" (generically, SUSY models tend to have more than one Higgs boson), is that it fixes one of two key constants from which supersymmetric particle masses are derived in these models, dramatically constraining the mass spectrum of the other particles and as a result, making falsification of the models from failure to find other supersymmetric particles in the expected mass ranges much easier.
This conclusion is somewhat overstated, since there are many variants of SUSY theories, not all of which derive the Higgs boson mass in the same way. But, the Higgs boson mass does provide an important calibration point for the mass scale of any SUSY theory.
For example, as one recently published paper explained:
In this paper, we explore the potential consequences for the MSSM and low-scale SUSY-breaking. As is well-known, a 125 GeV Higgs implies either extremely heavy stops (≳10 TeV), or near-maximal stop mixing. We review and quantify these statements, and investigate the implications for models of low-scale SUSY-breaking such as gauge mediation where the A-terms are small at the messenger scale. For such models, we find that either a gaugino must be superheavy or the NLSP is long-lived. Furthermore, stops will be tachyonic at high scales. These are very strong restrictions on the mediation of supersymmetry breaking in the MSSM, and suggest that if the Higgs truly is at 125 GeV, viable models of gauge-mediated supersymmetry breaking are reduced to small corners of parameter space or must incorporate new Higgs-sector physics.
Another such paper noted that the Higgs boson indirectly places an upper bound on supersymmetric particle masses:
The LHC is putting bounds on the Higgs boson mass. In this Letter we use those bounds to constrain the minimal supersymmetric standard model (MSSM) parameter space using the fact that, in supersymmetry, the Higgs mass is a function of the masses of sparticles, and therefore an upper bound on the Higgs mass translates into an upper bound for the masses for superpartners. We show that, although current bounds do not constrain the MSSM parameter space from above, once the Higgs mass bound improves big regions of this parameter space will be excluded, putting upper bounds on supersymmetry (SUSY) masses. On the other hand, for the case of split-SUSY we show that, for moderate or large tanβ, the present bounds on the Higgs mass imply that the common mass for scalars cannot be greater than 1011 GeV. We show how these bounds will evolve as LHC continues to improve the limits on the Higgs mass.
Another SUSY constraint from the Higgs search that deserves more attention than it has received in popular discussions so far is that all SUSY theories predict multiple Higgs bosons and the LHC Higgs boson search has excluded Higgs boson masses for the entire mass range much below 125 GeV and for masses as high as perhaps 600 GeV and soon approaching a full TeV. There are no signs of charged Higgs bosons yet. Any missing neutral Higgs boson would have to be either indistinguishably close to each other so that they look like a single kind of particle when in fact that are several particles that are quite similar to each other, or would have to be much heavier than the lighest Higgs boson. The constraints on additional SUSY Higgs boson masses are meaningful ones.
As an aside, the discovery of the Higgs boson was also a blow to "technicolor" theories, devised against the possibility that no Higgs boson would be discovered.
The Higgs boson discovery combined with other LHC searches has also essentially ruled out the SM4, a variation on the Standard Model with four rather than three generations of massive particles with each generation having a particle identical to the others in its generation except that it has a higher mass.
Other LHC Constraints On SUSY Theories
The LHC has not yet detected any superpartners or non-standard model particles. For example, spin 3/2 quarks have been excluded for masses of less than 490 GeV. The bounds on a minimum gluino mass have also continued to increase to about 1.24 TeV, in response to which theorists who not long ago were proposing a 600 GeV gluino have retreated to predictions of higher values for the mass of this hypothetical SUSY particle:
"Their most recent CMSSM SUSY “predictions” have gluinos at either 2000 GeV (hard for the LHC to see at full energy after 2014) or 4000 GeV (impossible for the LHC ever to see)."
From Not Even Wrong.
Similarly, refined details of B(s) meson decays confirmed to match Standard Model expectations in experiments have somewhat constrained the tan beta parameter of supersymmetry. Original scientific paper here. See also here.
[UPDATE: What is tan beta anyway and how precisely does it get involved? Jester explains this as follows:
But then SUSY has many knobs and buttons. The one called tanβ -- the ratio of the vacuum values of the two Higgs fields -- is useful here because the Yukawa couplings of the heavy Higgses to down-type quarks and leptons happen to be proportional to tanβ. Some SUSY contributions to the branching fraction are proportional to the 6th power of tanβ. It is then possible to pump up tanβ such that the SUSY contribution to Bs→μμ exceeds the standard model one and becomes observable. For this reason, Bs→μμ was hailed as a probe of SUSY.
But, at the end of the day, the bound from Bs→μμ on the heavy Higgs masses is relevant only in the specific corner of the parameter space (large tanβ), and even then the SUSY contribution crucially depends on other tunable parameters: Higgsino and gaugino masses, mass splittings in the squark sector, the size of the A-terms, etc. This is illustrated by the plot on the right where the bounds (red) change significantly for different assumptions about the μ-term and the sign of the A-term. Thus, the bound may be an issue in some (artificially) constrained SUSY scenarios like mSUGRA, but it can be easily dodged in more the general case.
END UPDATE]
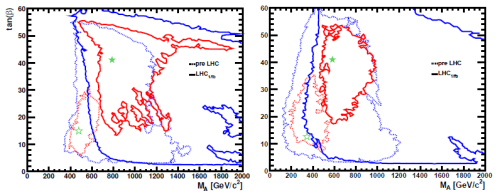
High energy physics blogger Matt Strassler providees a tan beta v. mass parameter "A" exclusion chart presented here together with some convenient background definitions. The money chart and caption from his blog post is as follows:
Fig. 2: as in Figure 1, except that the dashed lines give the constraints on the CMSSM and NUHM1 before the LHC began taking data, and the solid line gives the constraints after the data taken through early summer 2011 was analyzed. Notice the scale on the horizontal axis is different from that of Figure 1.
The LHC has also largely ruled out a large class of R-parity conserving SUSY models. Any SUSY theory where R-parity is not conserved, however, naturally implies a short proton decay half-life (which has never been observed experimentally and has been experimentally excluded to have a half life of at least about 13 billion years), and thus must have other features that suppresses R-parity violations to a low level.
In high energy physics blogger Matt Strassler's account in the wake of the Kyoto Conference results announced earlier this month:
[N]either CMS nor ATLAS sees any significant deviation from what is predicted by the Standard Model. And this now kills off another bunch of variants of many different speculative ideas. The details are extremely complicated to describe, but essentially, what’s dead is any theory variant that leads to many proton-proton collisions containing■two or more top quark/anti-quark pairs■multiple W and Z particles■two or more as-yet unknown moderately heavy particles that often decay to muons, electrons and/or their anti-particles■new moderately heavy particles that decay to many tau leptons
He also explains that:
Another point worth remembering is that the biggest “blows against” (cornerings of) supersymmetry so far at the LHC don’t come from the LHCb measurement [of B(s) meson decays]: they come from■the discovery of a Higgs-like particle whose mass of 125 GeV/c² is largely inconsistent with many, many variants of supersymmetry■the non-observation so far of any of the superpartner particles at the LHC, effects of which, in many variants of supersymmetry, would have been observed by nowHowever, though the cornering of supersymmetry is well underway, I still would recommend against thinking about the search for supersymmetry at the LHC as nearly over. The BBC article has as its main title, “Popular physics theory running out of hiding places“. Well, I’m afraid it still has plenty of hiding places.
Constraints From Neutrinoless Beta Decay Rates
The neutrinoless beta decay rate in MSSM is a function of the square of the LSP (lightest supersymmetric particle) mass times the square root of the gluino mass (there are also known constants that are figured into the relevant equation). See, for example, M. Hirsch (1995) and BC Allanach (2009). Any prediction of the MSSM in general in this regard certainly ought to apply to the Constrained MSSM (which, in fairness is pretty much ruled out already anyway on other grounds, for example, related to the implications of the discovery of a Higgs boson with its experimentally measured mass).
With an assumed 100 GeV LSP and 1000 GeV gluino, you expect neutrinoless beta production rates right on the boundary between what can be ruled out and what cannot be ruled out by the currently known experimental data.
At a 600 GeV LSP and a 2000 GeV-4000 GeV gluino (roughly speaking the current experimentally supported minimum masses of these supersymmetric particles if they exist at all), by way of comparison, the neutrinoless beta decay rate in the MSSM would be about 50-64 times as large as in a model with a 100 GeV LSP and 1000 GeV.
Neutrinoless double beta decay at this great a rate is easily ruled out by experimental data (even the data from the Moscow experiment whose alleged positive neutrinoless double beta decay results from Ge-76 isotype decays have been seriously questioned because other experiments have failed to replicate them). Indeed, even a four to eight fold increase in predicted neutrinoless double decay rates relative to that predicted for a 100 GeV LSP and 1000 GeV gluino in the MSSM is strongly disfavored by the existing experimental data tending to exclude neutrinoless double beta decay rates that high.
Non-detection of neutrinoless double beta decay also increasingly disfavors models of neutrino mass in which neutrino's derive their mass through interactions between other neutrinos (and in which a neutrino is its own antiparticle) in a "see-saw process" which are called Majorina neutrinos, in favor a neutrinos that acquire mass only via the means that other Standard Model fermions do, called Dirac neutrinos.
Models with massless neutrinos were definitively ruled out when the phenomena of "neutrino oscillation" was discovered, requiring a modification of the Standard Model, which had previously assumed that neutrinos were massless, to accommodate this reality.
Why Do Most SUSY Models Have Significant Lepton Number Violations?
Most SUSY models intentionally replace the Standard Model's lepton number conservation law (which prohibits neutrinoless double beta decay), with a law that conserves baryon number minus lepton number (B-L) instead, rather than preserving the two quantities separately. See generally, here.
For theorists, B-L conservation (and hence lepton number violations in some circumstances) is a feature rather than a bug, because it makes it easier to address the cosmology problems of leptogenesis and matter-antimatter asymmetry in the universe. But, any model that abandons the strict lepton number conservation law of the Standard Model also has to find a way to suppress lepton number conservation violations to the extremely low levels necessary to be consistent with the experimental evidence in some principled way.
SUSY theorists have mostly chosen to suppress lepton number violations that contradict experimental data by favoring supersymmetric particle mass parameters that are low enough to produce undetectable levels of lepton number violations. But, as the LHC increasingly excludes lighter supersymmetric particles, this strategy is increasingly problematic as the back of napkin calculations above show.
Any modification of a SUSY theory that tends to solve the excessive neutrinoless double beta decay predictions of the theory also tend to reduce its usefulness in explaining leptogenesis and matter-antimatter asymmetries in the universe.
The related phenomena of flavor changing neutral currents (FCNCs) has never been observed experimentally even in quite high precision experiments.
What's Left Of SUSY Parameter Space?
Basically, the only ways the you can get neutrinoless double beta decay rates consistent with experiment, given the LHC gluino exclusions, are:
(1) to assume that there is some ca. 100 GeV or less LSP that has escaped detection at Tevatron and the LHC somehow, or
(2) to use a Non-MSSM SUSY theory that produced much lower rates of neutrinoless double beta decay for some reason and otherwise fits new constraints better than minimal SUSY models.
So, if one is not going to reject SUSY (and many people already gravely doubt its viability as a theory) then, you have either have to be something of a high energy physics data denialist, or you end up with a SUSY model that doesn't look natural at all.
One can devise a non-MSSM SUSY theory that suppresses neutrinoless double beta decay, and one can likewise devise a SUSY model whose supersymmetric particles that are lighter than the top quark have properties that make them impossible for Tevatron or the LHC to detect with the experimental methods and data analysis techniques that were actually used in those experiments. But, most SUSY models are not designed to address these concerns and the Tevatron and LHC experiments have had no shortage of SUSY advocates involved in their experimental designs.
Matt Strassler argues that there could be a merely inaccessible SUSY theory out there:
[L]eft out of this discussion is the very real possibility that supersymmetry might be part of nature but might not be accessible at the LHC. The LHC experiments are not testing supersymmetry in general; they are testing the idea that supersymmetry resolves the scientific puzzle known as the hierarchy problem. The LHC can only hope to rule out this more limited application of supersymmetry. For instance, to rule out the possibility that supersymmetry is important to quantum gravity, the LHC’s protons would need to be millions of billions of times more energetic than they actually are. The same statements apply for other general ideas, such as extra dimensions or quark compositeness or hidden valleys.
In so far as he argues that supersymmetry could exist but be accessible only at energies far beyond those that the LHC can probe, I think that he is overlooking means of searching that provide an experimentally accessable bound on SUSY theories with very high characteristic energies such as neutrinoless double beta decay and the bounds imposed by the "discovered" Higgs boson mass, and by the non-discovery of the kind of dark matter particles that would be consistent with such theories. Certainly, LHC itself can't exclude high energy SUSY theories, but fundamental physics has more than one tool in its toolbox and is perfectly capable of applying different kinds of experimental bounds to the same problem.
Also, for clarity's sake, it is worth noting that SUSY theories proper, by definition, don't deal with quantum gravity. SUSY like theories that incorporate some kind of quantum gravity component are called SUGRA theories (an acronym for a set of theories normally described in full fledged words as "Supergravity" theories).
There are reasons to believe that gravity may be relevant to quantum physics at high energies. Indeed, one of the right on the button Higgs boson mass predictions was derived from assuming in a scheme called "asymptotic safety" that just such a thing (in an ad hoc heuristic way since there is no coherent and complete theory that integrates quantum mechanics and gravity) was the case and working backward from that assumption using otherwise Standard Model physics. But, there is no particular reason to think that the high energy gravitational effects on quantum physics should be "supergravity" effects.
Strassler's notion that ideas like extra dimensions, quark compositeness and hidden valleys might be accessible only at energies far in excess of those accessible at the LHC has more merit.
The LHC has excluded the existence of "large" extra dimensions of a particular types (e.g. Kaluza-Klein dimensions) that are present in many grand unified theories that would have particular phenomenological consequences if they existed, but the scale of the extra dimensions excluded is far larger than these extra dimensions are typically hypothesized to be, so this is unsurprising. Often these extra dimensions are hypothesized to exist with effective sizes corresponding to the GUT or Planck energy scales or something a bit larger than that, while the exclusions are far extra dimensions of these types that are many orders of magnitude larger.
The LHC has considerably increased an already very high experimental bound on quark compositeness (as an aside the illustration in the linked materials of fundamental particle masses in terms of animal weights to convey their relative masses is delightful - electron neutrinos, for example, are represented by ants, down quarks merit a penguin, taus a buffalo, and W and Z bosons are represented by blue whales). The exclusions are for distances and energies corresponding to six to eight TeV, higher than almost any of the other exclusions at the LHC.
As far "hidden valleys", suffice it to say that by definition, their hiddenness at lower energies makes them possible, but that the only phenomena that seems to motivate such a theory given current experimental data is cosmological inflation, in the earliest instants of the universe. This would be more like a cloud covered peak of the mountain than a "hidden valley."
Off topic:
An interesting preon paper was published last month in the journal "Modern Physics Letters A."

No comments:
Post a Comment