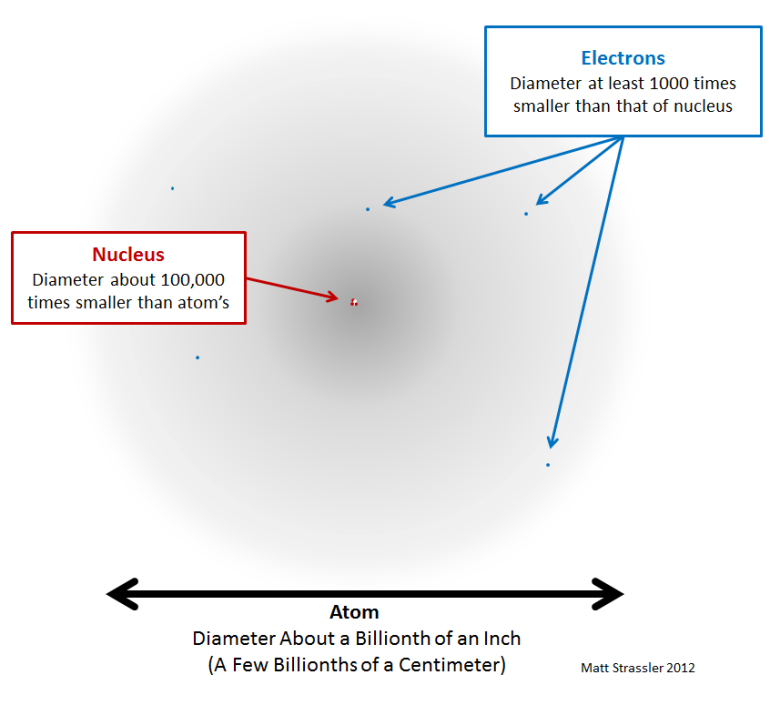
*
Dark Matter
Among the hints of dark matter, I believe that the three apparently decidedly non-background-like events seen by CDMS II represent the strongest hint of a dark matter particle we have seen so far.
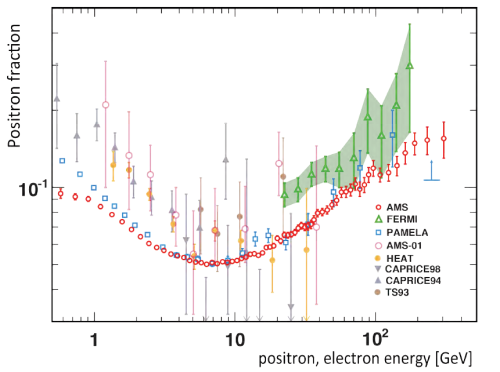
However, there are other hints, too. . . . CDMS suggests a WIMP mass of 8.6 GeV; AMS-02 indicates 300 GeV or more; and we also have the Weniger line at Fermi which would imply a WIMP mass around 130-150 GeV. These numbers are apparently inconsistent with each other.
An obvious interpretation is that at most one of these signals is genuine and the other ones – or all of them – are illusions, signs of mundane astrophysics, or flukes. But there's also another possibility: two signals in the list or more may be legitimate and they could imply that the dark sector is complicated and there are several or many new particles in it, waiting to be firmly discovered.
From
here.
Lubos Motl greatly understates the weight of the experimental difficulties facing potential dark matter particles in these mass ranges if these indications are anything more than experimental error or statistical flukes.
There are other contradictory results from other experiments at the same light dark matter scale as CDMS II. Some purport to exclude the result that it claims it sees and either see nothing at all, or see something else at a different mass or cross-section of interaction. One other experiments seems to confirm the CDMS-II result.
Even if there are dark matter particles, however, none of the hints of possible dark matter particles are consistent with the dark matter particle needed to explain the astronomy data which is why we need to consider that dark matter exists at all.
Hot Dark Matter (i.e. neutrinos) does not fit the astronomy evidence.
Cosmic microwave background radiation measurements (most recently by the Planck satellite which are as precise as it is theoretically possible to be in these measurements from the vicinity of Earth), establish that dark matter particles must have a mass signficantly in excess of 1 eV (i.e. it can't be "hot dark matter") and hypothesizes that a bit more than a quark of the mass-energy of the universe (and the lion's share of the matter in the universe) is full of of unspecified stable, collisionless dark matter particle relics of a mass greater than 1 eV.
Cold Dark Matter (e.g. heavy WIMPs) does not fit the astronomy evidence.
Simulations of galaxy formation in the presence of dark matter are inconsistent with "cold dark matter" of roughly 8 GeV and up of particle mass. Cold dark matter models, generically, predict far more dwarf galaxies than we observe, and also predict dark matter halo shapes inconsistent with those inferred from the movement of luminous objects in galaxies.
The conventional wisdom in the dark matter field has not necessary fully come to terms with this fact, in part because a whole lot of very expensive experiments which are currently underway and have many years of observations ahead of them were designed under the old dominant WIMP dark matter paradigm that theoretical work now makes clear can't fit the data.
Warm Dark Matter could fit the astronomy evidence.
The best fit collisionless particle to the astronomy data at both CMB and galaxy level is a single particle of approximately 2000 eV (i.e. 0.00002 GeV) mass, with an uncertainty of not much more than +/- 40%. This is called "warm dark matter."
There is not yet a consensus, however, that has determined if this model can actually explain observed dark matter phenomena. A particle of this kind can definitely explain many dark matter phenomena, but it isn't at all clear that it can explain all of it. Most importantly, it isn't clear that this model produces the right shape for dark matter halos in all of the different kinds of galaxies where these are observed (something that MOND models can do with a single parameter that has a strong track record of making accurate predictions in advance of astronomy evidence).
The simulations that prefer warm dark matter models over cold dark matter models also strongly disfavor models multiple kinds of warm dark matter, although some kind of self-interaction of dark matter particles is not ruled out. So, more than the aesthetic considerations that Lubos Motl discusses in his post disfavor a complicated dark matter sector.
This simulation based inconsistency with multiple kinds of dark matter disfavors dark matter scenarios in which the Standard Model is naively extended by creating three "right handed neutrinos" corresponding one a one to one basis with the weakly interacting left handed neutrinos of the Standard Model but have different and higher masses, with some sort of new interaction governing left handed neutrino to right handed neutrino interactions.
But, as explained below, any warm dark matter would have to be "sterile" with respect to the weak force.
These limitations on dark matter particles make models in which sterile neutrino-like dark matter particles arise in the quantum gravity part of a theory, rather than in the Standard Model, electro-weak plus strong force part of the theory, attractive.
Light WIMPs are ruled out by particle physics, although light "sterile" particles are not.
No dark matter particle that is weakly interacting of less than 45 GeV is consistent with experimental evidence. Any weakly interacting particle with less than half of the Z boson mass would have been produced in either W boson or Z boson decays. Moreover, if there were some new particle with a mass of between 45 GeV and 63 GeV that was weakly interacting, it would have been impossible to observe, as the LHC has to date, Higgs boson decays that are consistent with a Standard Model prediction that does not include such a particle to within +/- 2% or so on a global basis.
In other words, any dark matter particle of less than 63 GeV would have to be "sterile" which is to say that it does not interact via the weak force. This theoretical consideration strongly disfavors purported observations of weakly interacting matter in the 8 GeV to 20 GeV range over a wide range of cross-sections of interaction, where direct dark matter detection experiments are producing contradictory results.
It is also widely recognized that dark matter cannot fit current models if it interacts via the electromagnetic force (i.e. if it is "charged") or if it has a quantum chromodynamic color charge (as quarks and gluons do). This kind of dark matter would have too strong a cross-section of interaction with ordinary matter to fit the collisionless or solely self-interacting nature it must have to fit the dark matter paradigm for explaining the astronomy data.
So, sterile dark matter can't interact via any of the three Standard Model forces, although it must interact via gravity and could interact via some currently undiscovered fifth force via some currently undiscovered particle (or if dark matter were bosonic, via self-interactions).
Neither heavy nor light WIMPs fit the experimental evidence as dark matter candidates.
Since light WIMPs (weakly interacting massive particles) under 63 GeV are ruled out by both particle physics, and all WIMPS in the MeV mass range and up are ruled out by the astronomy data, the WIMP paradigm for dark matter that reigned for most of the last couple of decades is dead except for the funeral.
Even if there are heavy WIMPS out there with masses in excess of 63 GeV which are being detected (e.g. by the Fermi line or ASM-02 or at the LHC at some future data), these WIMPS can't be the dark matter that accounts for the bulk of the matter in the universe.
Direct detection of WIMP dark matter candidates is hard.
It is possible to estimate with reasonable accuracy the density of dark matter that should be present in the vicinity of Earth if the shape of the Milky Way's dark matter halo is consistent with the gravitational effects attributed to dark matter that we observe in our own galaxy.
So, for any given dark matter particle mass it is elementary to convert that dark matter density into the number of dark matter particles in a given volume of space. It takes a few more assumptions, but not many, to predict the number of dark matter particles that should pass through a given area in a give amount of time in the vicinity of the Earth, if dark matter particles have a given mass.
If you are looking for weakly interacting particles (WIMPs), you use essentially the same methodologies used to directly detect weakly interacting neutrinos, but calibrated so that the expected mass of he incoming particles is much greater. The cross-section of weak force interaction adjusted to fit constraints from astronomy observations such as colliding galactic clusters further tunes your potential signal range. You do your best to either shield the detector from background interactions or statistically substract background interactions from your data, and then you wait for dark matter particles to interact via the weak force (i.e. collide) with your detector in a way that produces an event that your detector measures, which should happen only very infrequently because the cross-section of interaction is so small.
For heavy WIMPs in the GeV to hundreds of GeV mass ranges the signal should be pretty unmistakable, because it would be neutrino-like but much more powerful. But, this is greatly complicated by a lack of an exhaustive understanding of the background. We do not, for example, have a comprehensive list of all sources that create high energy leptonic cosmic rays.
Direct detection of sterile dark matter candidates is virtually impossible.
The trouble, however, is that
sterile dark matter should have a cross-section of interaction of zero and never (or at least almost never) collide with the particles in your detector, unless there is some new fundamental force that governs interactions between dark matter and non-dark matter, rather than merely governing interactions between two dark matter particles. Simple sterile dark matter particles, which only interact with non-dark matter via gravity, should be impossible to detect directly following the paradigm used to detect neutrinos directly.
Moreover, while it is possible that sterile dark matter particles might have annihilation interactions with each other, this happens only models very very non-generic choices about their properties. If relic dark matter is all matter and not anti-matter, and exists in only a single kind of particle, it might not annihilate at all, and even if it does, the signal of a two particle warm dark matter annihilation which would have energies on the order of 4,000 keV would be very subtle and hard to distinguish from all sorts of other low energy background effects.
And, measuring individual dark matter particles via their gravitational effects is effectively impossible as well, because everything from dust to photons to cosmic microwave background radiation to uncharted mini-meteroids to planets to stars near and far contribut to the background, and the gravitational pull of an individual dark matter particle is so slight. It might be possible to directly measure the collective impact of all local dark matter in the vicinity via gravity with enough precision, but directly measuring individual sterile dark matter particles via gravity is so hard that it verges on being even theoretically impossible.
If sterile dark matter exists, its properties, like those of gluons which have never been directly observed in isolation, would have to be entirely inferred from indirect evidence.
*
The Higgs boson self-coupling.
One of the properties of the Standard Model Higgs boson is that it couples not only to other particles, but also to itself, with a self-coupling constant lambda of
about 0.13 at the energy scale of its own mass if it has a mass of about 125 GeV as it has been measured to have at the LHC (see also in accord
this paper of January 15, 2013). The Higgs boson self-coupling constant, like the other Standard Model coupling constants and masses vary based on the energy scale of the interactions involved in a systematic way based on the "beta function" of a particular coupling constant.
A Difficult To Measure Quantity
Many properties of the Higgs boson have
already been measured experimentally with considerable precision, and closely mathc the Standard Model expectation. The Higgs boson self-coupling, however, is one of the hardest properties of the Higgs boson to measure precisely in an experimental context. With the current LHC data set, the January 15, 2013 paper notes that “if we assume or believe that the `true’ value of the triple Higgs coupling lambda is true = 1, then . . . We can conclude that the expected experimental result should lie within lambda (0:62; 1:52) with 68% confidence (1 sigma), and lambda (0:31; 3:08) at 95% (2 sigma) confidence."
Thus, if the Standard Model prediction is accurate, the measured value of lambda based on all LHC data to date should be equal to 0.08-0.20 at a one sigma confidence level and to 0.04-0.40 at the two sigma confidence level.
With an incomplete LHC data set at the time their preprint was prepared that included only the first half of the LHC data to date, the authors were willing only to assert that the Higgs boson self-coupling constant lambda was positive, rather than zero or negative. But, even a non-zero value of this self-coupling constant rules out many beyond the Standard Model theories.
After the full LHC run (i.e. 3000/fb, which is about five times as much data as has been collected so far), it should be possible to obtain a +30%, -20% uncertainty on the Higgs boson self-coupling constant lamba. If the Standard Model prediction is correct, that would be a measured value at the two sigma level between 0.10-0.21.
BSM Models With Different Higgs Boson Self-Coupling Constant Values
There are some quite subtle variations on the Standard Model that are identical in all experimentally measureable respects except that the Higgs boson self-coupling constant is different. This would have the effect of giving rise to an elevated level of Higgs boson pair production while not altering any other observable feature of Higgs boson decays. So, if decay products derived from Higgs boson pair decays are more common relative to decay products derived from other means of Higgs boson production than expected in the Standard Model, then the Higgs boson self-coupling constant is higher than expected.
A recent post at Marco Frasca's Gauge Connection blog discusses two of these subtle Standard Model variants which are described at greater length in the following papers:
* Steele, T., & Wang, Z. (2013). Is Radiative Electroweak Symmetry Breaking Consistent with a 125 GeV Higgs Mass? Physical Review Letters, 110 (15) DOI: 10.1103/PhysRevLett.110.151601 (open access version available here).
This model, sometimes called the conformal formulation, predicts a different Higgs boson self-coupling constant value of lambda=0.23 at the Higgs boson mass for a Higgs boson of 125 GeV (77% more than the Standard Model prediction) in a scenario in which electroweak symmetry breaking takes place radiatively based on an ultraviolet (i.e. high energy) GUT or Planck scale boundary at which the Higgs boson self-coupling takes on a notable value (for example, zero) and has a value determined at lower energy scales by the beta function of the Higgs boson.
This model, in addition to providing a formula for the Higgs boson mass thereby reducing the number of experimentally measured Standard Model constants by one, dispenses with the quadratic term in the Standard Model Higgs boson equation that generates the hierarchy problem. The hierarchy problem, in turn is a major part of the motivation of supersymmetry. But, it changes no experimental observables other than the Higgs boson pair production rate, which is hard to measure precisely, even with a full set of LHC data that provide quite accurate measurements of most other Higgs boson properties.
Similar models are explored
here.
* Marco Frasca (2013). Revisiting the Higgs sector of the Standard Model arXiv arXiv: 1303.3158v1
This model predicts the existence of excited higher energy "generations" of the Higgs boson at energies much higher than those that can be produced experimentally, giving rise to a predicted Higgs boson self-coupling constant value of lamba=0.36 (which is 177% greater than the Standard Model prediction).
Both of these alternative Higgs boson theories propose Higgs boson coupling constant values that are outside the one sigma confidence interval of the Standard Model value based upon the full LHC data to date, but are within the two sigma confidence interval of that value. The 0.13 v. 0.23
Higgs self-coupling value distinction looks like it won’t be possible to resolve at more than a 2.6 sigma level even after much more data
collection at the LHC, although it should ultimately be possible to
distinguish Frasca's estimate from the SM estimate at the 5.9 sigma level
before the LHC is done, and a the 2 sigma level much sooner.
SUSY and the Higgs Boson Self-Coupling Constant
Supersymmetry (SUSY) models generically have at least five Higgs bosons, two of which have the neutral electromagnetic charge and even parity of the 125 GeV particle observed at the LHC, many of which might be quite heavy and have only a modest sub-TeV scale impact on experimental results.
The closer the measured Higgs boson self-coupling is to the Standard Model expectation, and the more precision there is in that measurement,
the more constrained the properties of the other four Higgs bosons and other supersymmetric particles must be in those models since the other four can't be contributing much to the scalar Higgs field in low energy interactions if almost all of the observational data is explained by a Higgs boson like looks almost exactly like the Standard Model one.
The
mean value of the Higgs boson contribution to electroweak symmetry breaking is about 96% with a precision of plus or minus about 14 percentage points. If the actual value, consistent with experiment is 100%, then other Higgs bosons either do not exist or are "inert" and do not contribute to electroweak symmetry breaking.