How Does The Standard Model Determine Mean Lifetimes For Hadrons?
In principle, all of these mean hadron lifetimes ought to be possible to calculate from first principles using Standard Model physics and its 26 or so experimentally measured constants (i.e. the four CKM matrix parameters, the four PMNS matrix elements, the three fundamental force coupling constants, and the fifteen experimentally measured fundamental particle masses, plus constants like the speed of light, Plank's constant, and pi which are not generally considered to be "Standard Model" parameters, in particular).
Generally, the essence of the way that this is done is by determining the potential strong and weak force decays available for each hadron considering the relevant conservation laws, then assigning a time estimate to each possible decay path that leads to decay products with lighter combined rest mass and expressing that number in the form of a decay width, and then adding up all of the available path specific decay widths in the correct way so that the total decay width can be determined and converted back to mean lifetime.
In general, the more mass-energy conservation permitted decays are available, the faster a particle will decay. The decay widths of each available strong force decay is generally about six or seven orders of magnitude larger than that of each available weak force decay, so the mix of available strong force and weak force decays that are available dramatically influence the rate at which decays take place.
To do this from first principles for any given particle would require you to first calculate the masses of each of the roughly 700 possible ground state hadrons and many more possible excited state hadrons to determine which decay paths were permitted by mass-energy conservation, but with the crutch of experimentally measured masses for all or almost all of the hadrons which could plausible be in the decay paths for heavier hadrons, this task becomes much more manageable.
In the case of an undiscovered particle, the physicist must first predict the mass of the particle itself, and then examine all decay channels fitting known potential decay products that are permitted by conservation laws, but must finally consider whether there are any other undiscovered particles which could plausible be a decay channel for the undiscovered particle being evaluated and if so, must estimate the masses of these particles as well.
Mass estimates for undiscovered particles can start with simple extrapolation of patterns from the masses of particles that have some similarities with the target particle, as Gell-Mann did back in 1964 with the Omega baryon, and then can be refined by first principles calculations using tools like lattice QCD, which are much harder to do, but provide a more rigorously supported justification for the predicted value if done with sufficient precision.
In practice, all of the values below are experimentally measured values, because it is currently easier to obtain experimental observables, like particle masses, than it is to calculate them with precision using QCD.
The Seven Stable and Metastable Particles (Lifetimes Greater Than 10-5 s)
Only seven kinds of composite or fundamental subatomic particles have a mean lifetime of more than 10-5 (i.e. one hundred thousandths) seconds.
The Two Stable Or Metastable Spin 1/2 Baryons
*The proton (stable). This is a spin 1/2 baryon made up of two up quarks and one down quark. This is the lightest possible baryon because less binding energy is required to bind a spin 1/2 baryon than a spin 3/2 baryon, and because it has the lightest possible spin 1/2 quark content, since the Pauli exclusion principle makes it impossible to have a three up quark baryon with spin 1/2. Furthermore, conservation of baryon number prohibits decays into lighter mesons with equivalent quark contents (something that is far less problematic for meson decays since mesons have zero baryon number).
*The neutron (which is stable when bound in a stable atomic nucleus, but has a mean lifetime of 880 seconds as a free particle). This is a spin 1/2 baryon made up of one up quark and two down quarks. Neutrons can decay to protons via beta decay, which involves the weak force, but not via the strong force, because neutrons are only slightly heavier than protons because the binding energy is very similar but the down quark is slightly heavier than the up quark (even though this difference is muddied by the translation of the constituent quarks with their masses into binding energy amounts) leaving no other available strong force decays that conserve baryon number.
The Five Stable Fundamental Particles
*The electron (stable). This is a fundamental particle in the Standard Model. As the lightest charged lepton, it cannot decay into anything lighter while still conserving charge and lepton number.
*The three kinds of neutrinos (whose stability is limited as the three neutrino flavors, electron, muon and tau, oscillate between each other in a process that is not yet fully understood). This is a fundamental particle in the Standard Model. Neutrino oscillations conserve charge, since all neutrinos have zero electric charge and conserve lepton number. Oscillations from lighter neutrino mass states to heavier ones require a conversion of energy into mass, but because all three neutrino types are so light, it doesn't take much kinetic energy to make an oscillation possible and neutrinos often have high kinetic energy relative to their rest mass.
*The photon (stable until it hits a charged particle). This is a fundamental particle in the Standard Model. Since it has zero mass to start with, it can't decay into anything else with less rest mass, although it can have significant electromagnetic energy that can be converted into charged particle-charged antiparticle pairs in the right circumstances.
The Four Most Stable Exotic Particles (Lifetimes Less Than 10-5 s And Greater Than 10-9 s)
The muon and three kinds of spin zero mesons (and their antiparticles) have mean lifetimes of more than 10-9 (i.e. one billionth) of a second.
The Muon, A Fundamental Particle
The mean lifetime of a muon, the second generation electron, which is a fundamental particle in the Standard Model, is on the order of 10-6 (i.e. a millionth) seconds. This is about 100 times as long as the three longest lived types of mesons discussed below. It can decay only via the weak force.
The Three Most Stable Mesons
The charged pion made of an up quark and an antidown quark, the charged kaon made of an up quark and an antistrange quark, and the long form of the neutral kaon consisting of the linear sum of a down quark and an antistrange quark (which appears only in combination with the short neutal kaon linear combination of the difference between that particle with a much shorter mean lifetime), all have mean lifetimes on the order of 10-8 seconds.
The Many More Ephemeral Exotic Particles (Lifetimes Less Than 10-9 s And More Than 10-25 s)
About a hundred other kinds of hadrons, tau leptons (i.e. third generation electrons), top quarks, W bosons and Z bosons all have mean lifetimes of less than a billionth of a second. Gluons are also effectively very short lived.
The Six Most Ephemeral Fundamental Particles
A tau lepton (i.e. a third generation electron) has a mean lifetime on the order of 10-13 seconds, which is similar to the longer lived B mesons, D mesons, and spin-3/2 baryons, and is about 100,000 shorter than that of the longest lived mesons. It decays much faster than the muon because its higher rest mass relative to the muon makes many more decay channels available to it than are available for the muon. For example, a tau is heavy enough to decay to a muon, an electron, or up to four pions (charged and neutral combined). But, muons are already muons so they can't decay to muons, and are lighter than pions. Decays involving muons and pions make up much of its branching fractions, and it is also heavy enough to have a significant minority of decays that involve decays to kaons, which are also heavier than muons. Tau leptons are also much lighter than W bosons, so the mass of the virtual W boson in tau decay does not place an upper boundary on its decay products.
The Higgs boson's mean lifetime has not been measured experimentally, but is predicted in the Standard Model to have a mean lifetime of 10-22 seconds - similar to that of many hadrons with aligned spins, and about 1000 times as long as that of the top quark, W boson and Z boson.
Gluons are in principle as long lived as photons, but in practice, are only exchanged between color charged objects at very short range while moving at the speed of light, so they are in existence for only a time period on the order of 10-24 seconds and certainly far less than 10-9 seconds.
The mean lifetime of a top quark (i.e. the third generation up type quark) is about 5*10-25 seconds, which is about ten times shorter than the shortest lived hadron. And, since theory dictates that this time period is too short for hadronization to occur, all hadrons should have longer mean lifetimes than the top quark.
The W boson and Z boson have mean lifetimes of about 3*10-25 seconds, i.e. about 40% shorter than that of the top quark (which makes since because W bosons are what makes top quark decays possible).
Decays of heavy fundamental particles are sensitive to the existence of undiscovered fundamental particles which could provide decay paths for the heavy particles, but only if the undiscovered fundamental particles have some quantum number that is present in the original particle or can produce pairs of particles in the ends state that cancel each other out with respect to this quantum number. For example, a quark with lepton number zero can produce leptons as decay products, so long as they come in lepton-antilepton pairs.
Of course, examining particle decay widths as a means of detecting new particles only works if the the new particle's decay widths can be measured fairly accurately. Often, relative decay width measurements are not adequate for this task because the existence of a new particle providing a new decay path doesn't necessarily materially change the relative frequencies of other available decay paths of the particle. Also, this technique is less sensitive to low branching ratio decay paths which often have the most massive sets of particles and are often therefore hardest to detect.
General Trends For Hadrons (i.e. Mesons and Baryons)
In general, hadrons in which the all of the component quarks have aligned spins (spin 1 mesons and spin 3/2 baryons) are much less stable than hadrons whose component quarks have maximally unaligned spins (spin 0 mesons and spin 1/2 baryons).
In spin 0 mesons and spin 1/2 baryons, in general, the presence of charm and bottom quarks is associated with shorter mean lifetimes. Likewise, higher generation charged leptons are shorter lived than lower generation charged leptons. But, this simple trend does not even extend to the case of spin 1 and spin 3/2 hadrons.
Similarly, while some of the longest lived hadrons are also among the lightest, and some of the heavier hadrons are fairly short lived, and there is probably some modest correlation between mass and mean lifetime for hadrons, there is not really a consistent relationship between mass and mean lifetime for hadrons. Hadrons with similar masses and similar quark contents can have dramatically different mean lifetimes.
Hadrons can have mean lifetimes much greater than lighter hadrons. For example, pions, one of the longest lived kinds of mesons, are seven times lighter than protons and neutrons, which are much more stable.
There is a roughly 16 order of magnitude range of mean lifetimes for exotic hadrons (i.e. excluding the proton and neutron), while there is only about a 2 order of magnitude range of exotic hadron masses (which includes the proton and neutron mass).
Exotic Baryons
The most stable exotic spin 1/2 baryons (i.e. spin 1/2 baryons other than the proton or neutron) have mean lifetimes on the order of 10-10 seconds or less, which is about 100 times shorter than the mean lifetime of the longest lived mesons.
The most stable spin 3/2 baryon, the Omega baryon which consists of three strange quarks, has a mean lifetime on the order of 10-11 seconds. The Omega baryon's mean lifetime is 1,000 times shorter than the longest lived mesons and 10 times shorter than the longest lived unstable spin 1/2 baryons, but 100,000,000,000 (i.e. 100 billion) times as long as any other spin 3/2 baryon. It's long life is explained essentially by the fact that the only available decays require one of the strange quarks to decay via the weak force into an up quark (typically into a uss baryon and an pi minus meson made of an antiup quark and a down quark that are produced in the decay of a W- boson emitted by one of the strange quarks as it became an up quark). Since all combinations of hadrons with exactly three strange quarks have higher masses combined than the Omega baryon, it cannot decay via the strong force.
The prediction of the Omega baryon's existence and properties with the quark model by Gell-Mann which was confirmed in 1964 was a major confirmation of that model (the model looked at a pattern in spin 3/2 baryons observing that there were four kinds of Delta baryons comprised only of up and down quarks that each had about the same mass, three kinds of Sigma baryons comprised of one strange quark and two up or down quarks that each had a mass about 152 MeV higher than the Delta baryons, two with two strange quarks and one up or down quark with about the same mass about 150 MeV higher than the Sigma baryons, and no candidates with three strange quarks. Gell-Mann followed the logical progression and guessed that the new sss baryon would have a mass 151 MeV higher than the previous layer of spin 3/2 baryons - in practice it turned out to be 152 MeV higher with the discrepancy being far less than margin of error in the measurement. At each step, it turns out, this involves about 90-100 MeV of strange quark mass and 50-60 MeV of additional gluon binding energy, although the strange quark mass wasn't known at the time.
As Hyperphysics explains, another step in the Omega baryon decay which also occurs only via the weak force, the decay of sigma baryons (see here), while for example a Delta++ baryon (three up type quarks) can easily decay via the strong force because its mass is greater than the sum of the proton (uud) and positively charged pion (u anti-d) with the same quark flavor numbers allowing it to decay via the strong force but with three sets of the lightest of the quark flavors does not easily decay via the weak force. This makes it possible to discern the strength of the weak force coupling constant relative to the strong force coupling constant:
The fact that the both the strong force and the weak force initiate decays of particles gives a way to compare their strength. The lifetime of a particle is proportional to the inverse square of the coupling constant of the force which causes the decay. From the example of the decays of the delta and sigma baryons, the weak coupling constant can be related to the strong force coupling constant. This application gives
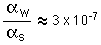 .
.
Since the strong coupling constant has a value of about 1 in the energy range around 1 GeV, this suggests a value for the weak coupling constant in the range
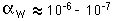 .
.Similarly, the slowness of charged pion and chaged kaon and long neutral kaon decay is attributable to the fact that all of these processes involve only weak force decays. This is not unrelated to mass. The charged pion is the lighest hadron, so its decays can only take place when the down quark or anti-down quark in the meson decays to an up quark of opposite matter-antimatter character to the other quark in the meson leaving no quark flavor numbers to conserve, because there are no lighter hadrons that preserve its quark content. They slow kaon decays, similarly, require a change in strangeness because there are no other hadrons with strange quarks lighter than this already light meson. But, the mass is relevant only in relation to other combinations of hadrons with the same amount of quark conservation, not in absolute terms.
All of the other spin 3/2 baryons (even those with only up and down quark content) have mean lifetimes on the order of 10-22 seconds or less, which is 100,000,000,000,000 (i.e. 100 trillion) times shorter than the longest lived mesons. This is surprising since the strange quark is the median mass hadronizing quark, rather than being at either the light or the heavy extreme. Presumably, spin 3/2 baryons without triplets of the same quark type decay quickly via the strong force because they have spin 1/2 counterparts with the same quark content which take less binding energy since the spins are balanced rather than aligned (there are no experimentally measured values for the properties of the bbb and ccc spin 3/2 baryons or for many other of the heavier quark content spin 3/2 baryons).
Delta baryons (which have spin 3/2) contain only up and down quarks, are the shortest lived hadrons of all, with mean lifetimes of about 5.58*10-24 seconds, while the other spin 3/2 baryons, which contain strange, charm and bottom quarks, have longer mean lifetimes for the reasons explained above.
Mesons
The longest lived spin zero B and D mesons have mean lifetimes on the order of 10-12 seconds or less, which is about 10,000 times shorter than the mean lifetime of the longest lived mesons. The other spin zero mesons (aka scalar and pseudoscalar mesons) that are not mentioned above (such as short neutral kaons, and various eta mesons) have mean lifetimes on the order of 10-11 seconds or less, but are generally longer lived than spin 1 mesons.
The longest lived vector mesons (those with spin one) have mean lifetimes on the order of 10-20 seconds or less, which is about 1,000,000,000,000 (i.e. a trillion) times shorter than the mean lifetime of the longest lived mesons. Their greater mass, relative to quark content, makes strong force decay routes to lower spin mesons (for example) available in most cases. For example, the charged rho and charged pion both have quark contents of an up quark and an antidown quark. But, the charged rho has a mass of about 775 MeV while the charged pion has a mass of about 139.6 MeV. Given that the quark mass in both cases is about 10 MeV, the charged rho has gluonic binding energy of about 765 MeV while the charged pion has gluonic binding energy about about 130 MeV, so the rho takes about 5.6 times as much energy to hold together as the pion.
The shortest lived vector mesons have mean lifetimes on the order of 10-24 seconds for the charged and neutral rho mesons (made up of only up and down quarks), and of 10-23 seconds for the Omega meson (which is the long form of the neutral rho meson); while vector mesons with heavier constituent quarks are longer lived.
General Considerations and Observations
Five Flavors Of Quarks Have No Mean Lifetimes In Isolation
None of the quarks, other than the top quark, has a mean lifetime that is a meaningful number. Their mean lifetimes are very dependent upon the kind of hadron in which they are confined. The more binding energy a hadron has, the more likely it is that it will have many options to decay into products that conserve quantum numbers while involving less mass. The presence of heavy quarks in a hadron can also increase the amount of mass that can be present in an end state and thereby make more decay routes available, but only at the cost of making decay products that preserve quantum numbers without flavor changing weak force interactions which proceed more rapidly scarce.
For example, an up quark in a proton is perfectly stable, while an up quark in a three up quark Delta baryon, Rho Meson or Omega meson is highly unstable. A down quark in a proton is perfectly stable, but a down quark in a free neutron has a mean lifetime of 880 seconds. An Omega baryon, with three strange quarks, is much longer lived than some baryons with fewer strange quarks.
On the other hand, no hadron containing a second or third generation quark is stable, because mass reducing weak force decays are always possible in that situation, even though they are slower than strong force decays. No hadron containing even a single strange quark has a mean lifetime of more than 10-8 seconds. No hadron containing even a single charm or bottom quark has a mean lifetime of more than 10-12 seconds. Since the slowest hadron decays generally involve cases where only the weak force is available to bring about the decays, these times are reasonable proxies for the characteristic weak force decay time period for these heavy quarks.
Presumably, the mean lifetimes of quarks other than the top quark when unconfined (e.g. at the instant that they come into being during Z boson decay) is longer than the time required for hadronization, but this number is basically counterfactual as all quarks other than top quarks are always observed in a confined state.
Impact of Hadronic Molecular Binding
As noted in the previous post, there are indications that "hadronic molecules" akin to atomic nuclei can form from pairs of B mesons and from pairs of D mesons. Neither of these "hadronic molecules" is stable and it isn't clear if this form of bonding has an impact on mean meson lifetime, although the comparable phenomena in atomic nuclei, clearly does have the capacity to extend the mean lifetime of a neutrino in some circumstances.
Certainly, there is no theoretical expectation at this time that some otherwise unstable exotic meson or baryon could be even metastable with a mean lifetime as long as a muon by virtue of being part of such a "hadronic molecule", although this is in part because there is very little theoretical work that has been done on the subject.
Mean Lifetime Is An Inverse Function Of Total Decay Width
For those so inclined, mean lifetimes can be converted to total decay widths as follows: mean lifetime equals reduced Planck's constant h divided by total decay width gamma.
Particles With Identical Lifetimes Are Treated As One Particle For These Purposes
At least at the level of precision involved in this post, in the Standard Model, particles and antiparticles have the same mean lifetimes. Therefore, particles and antiparticles are not counted as different particles for the purposes of this post and are not separately discussed. Similarly, other particles which are indistinguishable for purposes of mean lifetime (such as different parity versions of fermions, and the eight different kinds of gluons) are treated as one kind of particle for these purposes.
An Aside On Proton Decay
As an aside, a very large share of all beyond the Standard Model theories, and grand unification theories (GUTs) in particular, call for the proton to be unstable, even though proton decay (for example, into a neutral pion and a positron, which have the same charge and spin and lower mass, but which would violate baryon number conservation and is therefore absent from the Standard Model).
Proton decay has never been observed. The experimental bound on the minimum mean lifetime of a proton is about 1034 years. By comparison, the age of the universe is approximately 1010 years, so the number of protons that have decayed since they formed over the lifetime of the universe is not more than one in 1024. By comparison, there are approximately 3.5*1079 protons in the universe (of which fewer than one in 1010 are antiprotons). The mean proton lifetime is at least 1036 times as long as the mean lifetime of a free neutron. The mean proton lifetimes is at least 1062 times as long as the shortest observed mean hadron lifetime, which is very close to the minimum theoretical minimum hadron lifetime due to the minimum time necessary for hadronization revealed by the top quark's inability to hadronize.
Personally, I have a low opinion of beyond the Standard Model theories that claim, as some do, that proton decay in a manner that does not conserve baryon number occurs at a very low, but non-zero rate just beyond current detection limits, such as 1036 years.
No comments:
Post a Comment