I have added theory blog of Mitchell, who frequently comments regarding physics posts at this blog, to the blog roll and removed a blog from a leading physics lab. This is because Mitchell, while making only a few posts a month at his blogs, points out interesting theoretical speculations and conjectures that other sources miss, while the lab's blog's posts frequently came long after news had broken elsewhere and added little or nothing to the discussion by true blogger run blogs. I run though all the links on this blog at least once a month and never found anything worth posting about at the link that I deleted.
The LC & P Paper Relationship
In particular, I'd like to note a recent post culminates a series that he's been making about empirical relationships of fundamental particle masses and the Fermi constant observed in a simple four page paper by Lopez Castro and Pestieau, that he calls the LC & P paper.
As background, "in the standard model, as set out e.g. in equations 1.4 and 1.14 in this thesis
mW= 1/2 g v
mZ= 1/2 sqrt(g'2+g2) v
where g is the SU(2)L coupling, and g' is the U(1)Y coupling."
The LC & P paper observes that the sum of the square of the mass of each of the fundamental bosons in the Standard Model is equal to the sum of the square of each of the fundamental fermions in the Standard Model, and that combined that they are equal to the square of the Higgs vacuum expectation value. As LC & P explain:
Using mH = (125.6±0.4) GeV and mt = (173.5±0.9) GeV and other masses from the PDG compilation, the left-hand side of Eq. (1) is in full agreement with the right-hand side because v^2 = 1/(√2GF ) = (246.2 GeV)^2.As Wikipedia explains, the Fermi coupling constant is itself of function of the W boson mass and the weak force coupling constant:
The strength of Fermi's interaction is given by the Fermi coupling constant GF. The most precise experimental determination of the Fermi constant comes from measurements of the muon lifetime, which is inversely proportional to the square of GF.[8] In modern terms:[4]
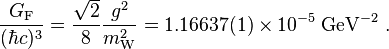
Here g is the coupling constant of the weak interaction, and mW is the mass of the W boson which mediates the decay in question.
In the Standard Model, Fermi's constant is related to the Higgs vacuum expectation valueThis coincidence is somewhat less impressive when one recognizes that only three of the twelve fundamental bosons have any rest mass; the photon and the eight varieties of gluons are massless. Similarly, the sum of all of the terms in the fundamental fermion part of this equation is smaller than the margin of error in the currently measured square of the top quark mass.[9]
Disregarding the terms that make only a negligible contribution to the total, the sum of the square of the W boson mass, plus the square of the Z boson mass, plus the square of the Higgs boson mass, plus the square of the top quark mass equals the square of the vacuum expectation value of the Higgs field to within current mass measurement experimental limits.
The masses of the W boson and Z boson, the numerical value of the weak force coupling constant and Fermi's constant are all known to a precision of about ten parts per million of more, while the measurements of the Higgs boson and top quark masses are known about one thousand times less precisely. If this relationship turns out to be only approximate when greater precision is available, it is less interesting.
Note also that the Z boson mass is a function of the W boson mass and the Weinberg angle, and that as noted previously at this blog, empirically, the Higgs boson mass is very close to 2H=2W+Z.
Thus, the collective mass scale of the Standard Model fermions (with their internal relative masses following Koide triple relationships with each other in many cases), and the collective mass scale of the Standard Model bosons, can each be understood as a function of the W boson mass, the weak force coupling constant, and the Weinberg angle, to the extent that the empirical 2W+Z=2H empirical mass relationship is exactly true.
If the sum of square of masses of empirical coincidence is also exactly true, then it is also true that:
"If one divides Eq. (1) by v^2 it yields:
2λ +g^2/4+(g^2 + g′^2)/4+sum over all fundamental fermion yukawas of (yf^2/2)=1, (2)
λ, g, g′ and yf being, respectively, the effective and renormalized scalar, gauge and Yukawa couplings."
The λ and yf are trivially functions of mass via the Higgs mechanism is which the mass of the of Higgs boson is a function mostly of its self-interaction term, and the masses of the fundamental fermions are a function of how strongly they interact with the Higgs field. But, described in this form, the masses of the fundamental particles come across almost as decay products of the Higgs vev allocated by a unitary vector whose elements are related trivially to the coupling constants of the electro-weak sector.
Implications for the functional relationship λ(g, g').
If the bosonic and fermionic contributions to the Higgs vev are identical, then 2λ +g^2/4+(g^2 + g′^2)/4=sum over all fundamental fermion yukawas of (yf^2/2) exactly or very nearly.
If 2λ +(g^2)/4 + (g^2+g′^2)/4=1/2 (which it would if the contributions were equal), it follows trivially that λ is a function of g and g'. Specifically, λ=1/4 -(g^2)/4- (g′^2)/8, (3). .
Since g is approximately 0.0072973525376 (roughly 1/137) and g' is approximately 10^-6 (so (g'^2)/8 is about 1.25*10^-13 and makes a negligible contribution to λ in (4)), so this would imply λ is equal to approximately 0.249986687. This is double a λ of 0.13, which is considered the Standard Model value. This could mean that I missed a factor of two somewhere in the math, or it could be the predicted value given masses close to what are observed is double the Standard Model prediction. The results are robust to me reversing g and g'. This is a strong, specific and falsifiable prediction of the conjecture articulated by LP & C, assuming that I have done the algebra correctly, which is similar to the prediction made by other means in this paper.
If the Standard Model prediction is accurate, the measured value of λ based on all LHC data to date should be equal to 0.08 to 0.20 at one sigma confidence level and 0.04 to 0.40 at the two sigma confidence level, so this value would be considerably less than two sigma from the current best estimate of the measured value and is certainly not ruled out experimentally in these early days.
Under the weaker assumption that (2), but not (3) is accurate, the Higgs boson scalar coupling constant and treating g and g' as fixed, λ is a function of the proportion of the Higgs vev that is attributable to bosonic rather than fermionic contributions and λ(sum(mB^2)/sum(mF^2)) and sum(mB^2)/sum(mF^2) must be quite different for
While sum(mB^2)/sum(mF^2) may not equal precisely 1 as hypothesized, given that the error in mB is less than +/-1% and that the error in MF is less than +/-1%, the possibility that sum(mB^2)/sum(mF^2) is so far off seems implausible, as does the possibility that sum(mB^2)+sum(mF^2)=v^2 is off by more than a few percent.
Thus, even if the relations in (1) and (2) are merely approximate, rather than exact, if it is not a total coincidence, even if it is an oversimplification, the Standard Model implication would seem to be that λ is at the high end of the range of experimentally measured possible values, given the masses of the various fundamental particles. I'm not a professional physicist, of course, and I may be missing a moving part or obvious problem with this analysis somewhere. As always, comments and corrections are welcome.
[Corrected mathematical mistake on August 12, 2013; corrected error in name on August 13, 2013.]
Other observations
These quite simple relationships manage to coexist with the fact that the conventional Standard Model relationship between the W boson mass, the Higgs boson mass and the top quark mass also holds to within current experimental limitations.
The symmetry of masses between the bosons and the fermions supports, and perhaps sheds light on, the inference that the symmetry that SUSY puts in obviously and by hand between bosons and fermions, may already exist for some far less obvious fundamental reason in the Standard Model (thus rendering SUSY superfluous).
This analysis also reinforces the notion that strong force interactions have nothing to do with fundamental particle masses, which seem to be entirely a function of electro-weak interactions, even though strong force interactions account for most of the masses of composite quark matter like protons and neutrons.
UPDATE August 13, 2013:
Torrente-Lujan noted in a September 10, 2012 pre-print that mZ*mt/mH2 was 1.0022+/-0.007+/-0.009. In other words, that it was well within margins of experimental error of unity. He used the following data points:
mZ = 91.1876 +/- 0.0021 GeV/c2;
mt = 173.5 +/- 0.6 +/- 0.8 GeV/c2; and
mH = 125.6 +/- 0.4 +/- 0.5 GeV/c2.
This estimate of mt is a bit higher than the current error weighted world average but not enough, given the uncertainty, to rule out the relationship.
If the ratio is exactly one and other values were as used in that preprint, mH would need to be 125.8 GeV/c2.
It is also interesting, or at least equally amusing, to consider an alternative way to express the closeness of the ratio p t to one. If we consider the individual mass ratios mZ/mH; mH/mt, their current experimental values are mZ/mH= 0.726 +/- 0.003; mH/mt= 0.724 +/- 0.005. . . . Somehow the mass of the "lowest" scalar particle mass is the geometric mean of the highest spin 1 and spin 1/2 masses.Again, a hint of the Higgs boson and field's possible role in balancing fermionic and bosonic Standard Model particles, giving rise to a fermion-boson superishsymmetry without the extra particles.
The rest of the discussion is also interesting. Don't forget, for example, that g'=g*tan(Weinberg Angle) in the Standard Model.

11 comments:
I hadn't noticed the remark about "almost equal contributions of fermions and bosons".
btw "Lopez Castro" is one name.
Thanks, I hadn't caught that.
In raw numbers (mean and one SD):
mW^2=6464 (6460-6468)
mZ^2=8315 (8315-8316)
mH^2=15775 (15675-15876)
mw^2+mZ^2+mH^2=30554 (30450-30666)*
* this is a crude sum of high and low estimates, the correctly summed error ranges is slightly lower. But, since almost all of the uncertainty is from the Higgs (on the high end 4W+1Z+101H; on the low end 4W+0Z+100H), the impact of not using the proper formula is minimal.
mt^2=30102 (29791-30415)
The sum of the squares of the masses of the other five quarks, three charged leptons and three neutrinos is about 22.4 at best estimate with a sum of high end 1SD estimates being as much as 28.5 and low end estimates as low as about 21.6
Thus the fermionic contribution is about 30124 (29812-30444).
Thus bosonic and fermionic contributions 1SD ranges almost overlap. The mean mass square sum values differ by about 1.4% which is equivalent to a 0.7% difference in the underlying masses.
The sum of all values is 60678 (60262-61110), This translates into a predicted Higgs vev of 246.33 (245.48-247.20) vs. an actual value of 246.22 (with an error of less than one in the final digit). This is a difference from the mean of 0.04% of the Higgs vev value which is well within the error bars.
One more point there: this analysis tends to favor a lowish Higgs mass within the existing error bars, and a top quark mass that is a bit higher than the mean estimate but is off by less than the Higgs estimate.
Taking the fermionic and bosonic contributions to be exactly equal, using the low end values within 1 SD for the W and Z mass (which have only slight impact) and assuming the Higgs vev to be accurate to five significant digits, the predicted value for the top quark mass is 174.0 GeV (well within 1 SD), and the predicted value of the Higgs boson mass is 124.6 (which is 2.5 SDs below the current mean estimate).
The formula 2W+Z=2H yields a prediction for the Higgs boson mass of about 125.99 +/- 0.02, which is within 1 SD of the currently measured value.
An equal bosonic and fermionic contribution to Higgs vev is inconsistent with an exact 2W+Z=2H formula, since they demand Higgs masses approximately 1.4 GeV different from each other. Since the exact 2W+Z=2H formula is better supported empirically than the equal bosonic and fermionic contribution formula and both can't simultaneously be true, lets assume that 2W+Z=2H is true and that equal contributions is only approximate and is not exactly true.
Assuming that the W mass is at the low end of the current range (which global fits suggest) for a W mass of say 80.376 instead of 80.399, you would get a 2W+Z=2H prediction for Higgs boson mass of 125.97 GeV. This would imply a top quark mass (on the sum of fundamental particle masses squared equals the Higgs vev formula) of 173.1 (unaffected at four significant digits by uncertainty in other fermion masses). Both of these numbers are within 1 SD of the currently measured values and would be consistent with the W-t-H global fit using Standard Model relationships. These value would leave the geometric mean relationship of Z/H v. H/t unequal with 0.724 in the first case and 0.728 in the second.
A low end value for the W boson mass of 80.376 would imply a Higgs vev of 246.29 (v. 246.22 accepted value). This would allow for a top quark mass as high as 173.2 GeV.
At the current Higgs boson estimate (125.6) and the current top quark mass estimate (173.5), with a W value of 80.376 and a corresponding adjustment to 246.29 of the Higgs vev, the different between the LC&P sum of fundamental particle masses squared and the Higgs vev squared narrows to 60,674 GeV^2 (sum of particle masses squared) v. 60,659 (Higgs vev squared) which is a difference of just 0.02% of the Higgs vev, a very close agreement indeed are far within experimental measurements possible in the foreseeable future (but still not enough to make fermionic and bosonic contributions equal and 2W+Z=2H at the same time).
Query if a slight running of masses or coupling constants could produce a 50-50 bosonic and fermionic contribution which is currently about 1% off, roughly the difference between pole mass and Z scale mass for a top quark, but maybe not quite that much.
per this paper it looks like the values that I used for g and g' were off considerably because I used the raw coupling constants like alpha without making a 4pi and a sin of the weinberg angle adjustment, which combined increases g by a factor of about 50.
Using values of g^2=0.3963962702
and g'^2=0.2287192211 which are in turn based upon g^2=4pi(alpha)/sinW and g'^2=gtanW where sinW=0.23122 and tan W=0.5769964004(using an input of 3.14/6 radians), I recover lambda = 0.1223110298 which is very close to the Standard Model expected value of about 0.13 to two significant digits, particularly considering that I am using 3 significant digit approximations for pi and two significant digit approximations for tan W.
Some of the key relationships are spelled out here.
Post a Comment