Overview
I mention this hypothesis set forth in a 2009 linguistics paper for completeness, but don't give it that much credit.
I am inclined to favor the majority view that Ainu is a language isolate, with linguistic family connections too remote in time to be discernible through linguistic analysis of modern or historically attested languages.
Still, it is credible enough and corroborated enough by other evidence that it shouldn't be dismissed out of hand either.
The Genetic And Archaeological Evidence
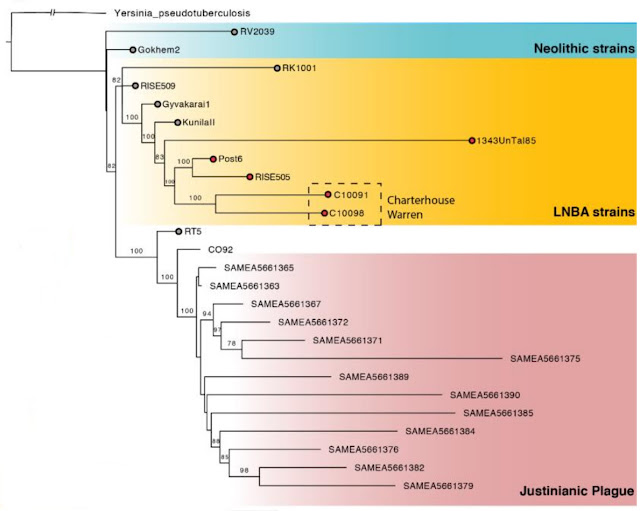
The genetic data (through no fault of the authors of this 2009 piece which had much less genetic evidence at its disposal) and related physical anthropology data referenced in the paper needs to be pretty much ignored in favor of better quality and more recent data and anthropological work (e.g. in 2012, 2013 and 2021). My linked analysis of a state of the art 2021 paper's findings notes that: A TreeMix analysis places the Jomon as an offshoot of the Hoabinhian people (a Mesolithic wave of people in Southeast Asia and Southern China ca. 12,000 to 10,000 BCE), with the Kusunda people (who are hunter-gathers in Western Nepal who historically spoke a language that is an isolate and were animistic religiously) as an intermediate population.
Y-DNA haplogroup D has a cryptic distribution found in isolated pockets across Asia including Siberia and Tibet that tends to favor a Northern route origin.
The mtDNA haplogroups N9b and M7a also tell story so deep in history (both are very basal in the Eurasian mtDNA tree and derived from African mtDNA haplogroup L3) that it is hard to reconstruct. Both mtDNA M and mtDNA N show distributions that tend to favor a Southeast Asian route to Japan, but perhaps this is because the northern bearers of this haplogroup went extinct, and were then almost fully replaced in the Last Glacial Maximum.
More up to date genetic data certainly favors the Austric hypothesis of this paper over an Altaic hypothesis, that the paper's authors reject on linguistic grounds.
But the genetic data is really agnostic between the possibility that the Ainu language is a language isolate, and the hypothesis that it could have a common source proto-language with the Austroasiatic and Austronesian languages that have "homelands" in Southeast Asia and Southern China.
The genetically and archaeologically supported time frame in which the Jomon people were isolated from mainland East Asia tends to favor, instead, the language isolate hypothesis, because the common language family connection of an "Austric" language family that would be consistent with the archaeological and genetic evidence would be deeper in the past than the common protolanguages shared by any other linguistically reconstructible language families.
If the word lists are as solid as claimed by the authors of this paper, the common ancestor of the Austric languages should have started to break up into the predecessors of the modern language families something like 3,000 to 6,000 years ago, or so (a time depth comparable to the one separating the most distinct of the Indo-European languages from each other, for example), rather than the at least 15,000 years of isolation suggested by genetic data and paleoclimate data (about the time depth probably uniting the pre-Columbian Native American languages of the Americas other than the language families that include the Na-Dene and Inuit languages, i.e. AmerInd, that are impossible to unite in their modern forms with linguistic information alone by any common linguistic characteristics).
On the other hand, as fishermen who had some outposts of their civilization as distant as the Ryukyu Islands, it is conceivable that they could have had maritime trade with East Asia that could have resulted in language shift, although the genetic data for the Jomon and Ainu people while supporting some links to Northeast Asia, do not support significant cultural or population genetic ties to Southern China and beyond from about 15,000 years ago to about 3,000 years ago).
Linguistic Evidence
The heart of the piece are the 88 suggested correspondences with Ainu or Proto-Ainu words that they identify, including eight pronouns, the numbers one through four (in five variations), and seventy-five other core vocabulary words.
Also, the correspondences listed also tend to support a coherent "Austric" grouping including Austroasiatic, Austronesian, and Thai-Kadai (at least). Other linguistic and genetic evidence favors the Austroasiatic and Hmong-Mien grouping.
These are respectable sized word lists, although I lack the expertise to critically evaluate the credibility of the "solid" and "doubtful" cognates on the list, which is where my doubt about the credibility of the authors is implicated.
The Russian school of linguistics, of which Blazek is a member and the journal this article comes from is a part, is notorious for lumping together languages into language families, like Nostratic, without solid evidence to back up the classification. And, the Sante Fe Institute, which is Bengtson's academic affiliation, also has a track record of low quality linguistic scholarship.
The Word List Details
All but one of the thirteen pronouns and numbers have solid suggested word-list correspondences from the Austroasiatic Mon-Khmer language (the comparison for the number 3 is doubtful), as do forty of the seventy-five other core words (with another nine more doubtful correspondences). Of the words that do not have a solid Mon-Khmer cognate, they identify another five core vocabulary words have an Austroasiatic Munda correspondence (usually accompanying a more doubtful Mon-Khmer cognate). In all there are 57 Ainu-Austroasiatic correspondences identified with another ten doubtful correspondences. The eight corresponding pronouns, as especially core words, would suggest a closer relationship between Ainu and Austroasiatic than with Austronesian, despite a slightly higher solid correspondence count for Austronesian.
They identify solid Austronesian, or Austronesian Asli correspondence for eight of the thirteen numbers and pronouns (half of the pronouns and the number four are absent), and another fifty-three core vocabulary words, including twenty-nine without a solid Austroasiatic cognate. In all there are 61 solid Ainu-Austronesian correspondences identified and another three doubtful correspondences (including one pronoun).
There are thirty-two correspondence present in both Austroasiatic and Austronesian, a roughly fifty-percent overlap.
There are 35 of eighty-eight words that have solid Thai-Kadai cognates (including eight of thirteen pronouns and numbers), but just five core words (or no numbers or pronouns) that have solid Thai-Kadai cognates but not solid Austroasiatic or Austronesian cognates ("evening", "rain", "river", "stone" (one of two Ainu words with this meaning), and "year"), with "evening" and "river" having doubtful Mon-Khmer correspondences.
They identify no solid cognates for words that do not have a solid Mon-Khmer, Munda, Austronesian, or Thai-Kadai correspondence on their word-list.
None of their correspondences are exclusively Hmong-Mien or Nihali.
There are 17 of eighty-eight words that have solid Hmong-Mien correspondences (including three of eight pronouns, and just one number (one of two forms of 2) and thirteen other core words ("child", "die", "earth", "egg", one of three forms of "eye"/"eyebrow", "fire", "lake"/"deep water", "mouth", "five"/"palm of hand", "rain", one of two forms of "stone", "vulva" and (fresh) water"). Of these seventeen words, just six lack a Mon-Khmer counterpart ("die", "egg", "lake"/"deep water", "rain", "stone" and "vulva").
The are only 3 solid Nihali correspondences ("fire", "tooth", and one of three variants associated with "eye"), each of which also have solid Mon-Khmer correspondences. This suggests that Nihali is a weak candidate for an overall "Austric" family grouping, as proposed tangentially in this paper, although it is a special case as the Wikipedia article on it that is linked above explains that its superficial dissimilarity from other Austroasiatic languages may be a deliberate ruse:
Franciscus Kuiper was the first to suggest that Nihali may be unrelated to any other Indian language, with the non-Korku, non-Dravidian core vocabulary being the remnant of an earlier population in India. However, he did not rule out that it may be a Munda language, like Korku. Kuiper suggested that Nihali may differ from neighbouring languages, such as Korku, mostly in its function as an argot, such as a thieves' cant. Kuiper's assertions stem, in part, from the fact that many oppressed groups within India have used secret languages to prevent outsiders from understanding them.
Linguist Norman Zide describes the recent history of the language as follows: "Nihali's borrowings are far more massive than in such textbook examples of heavy outside acquisition as Albanian." In this respect, says Zide, modern Nihali seems comparable to hybridised dialects of Romani spoken in Western Europe. Zide claims that this is a result of a historical process that began with a massacre of Nihalis in the early 19th century, organised by one of the rulers of the area, supposedly in response to "marauding". Zide alleges that, afterwards, the Nihalis "decimated in size", have "functioned largely as raiders and thieves ... who [have] disposed of ... stolen goods" through "outside associates". Zide adds that Nihali society has "long been multilingual, and uses Nihali as a more or less secret language which is not ordinarily revealed to outsiders" and that early researchers "attempting to learn the language were, apparently, deliberately rebuffed or misled".
The paper
There have been several attempts to solve the question of the genetic affiliation of the Ainu language of Hokkaido, formerly spoken also in Sakhalin and the Kuril islands. Apart from some inadequate or unlikely proposals there are two principal serious hypotheses: (1) Altaic, or more inclusively ‘Euroasiatic’ (Nostratic), as advocated for instance by Ramstedt, Koppelmann, Street, Patrie, Krippes, and Greenberg (with Ruhlen); and (2) Austronesian and Austroasiatic (plus Thai-Kadai and Miao-Yao, together Austric): e.g., Gjerdman, Sternberg, Murayama, and Vovin. Physical anthropology has been ambiguous on this question, in some aspects favoring a Northeast Asian, in others a Southeast Asian origin of the Ainu. The authors of the present article prefer (2), the Austric hypothesis, assuming an internal structure of the Austric macro-phylum consisting of Austro-Thai (Austronesian + Kadai), Miao-Austroasiatic (Hmong-Mien + Austroasiatic), and the peripheral remnants Nihali (in India) and Ainu. This article contains eighty-eight etymologies that the authors believe are strong evidence for the Austric affinity of the Ainu language. The lexical material includes personal pronouns, lower numerals, and other core basic vocabulary. Most importantly, this article is intended to stimulate discussion of the position of Ainu in genetic classification.
John D. Bengtson and Vaclav Blazek, "Ainu and Austric: Evidence of a Genetic Relationship" 2 Journal of Language Relationship 1-24 (2009).
From the body text at pages 1-3 and 19:
The Ainu language is known from Hokkaido, Sakhalin and the Kuril islands (where it is now
extinct). According to toponymy, Ainu was also formerly spoken on Honshu (Hudson 1994,
242–44), and apparently on other islands of the Japanese archipelago, probably even as far as
the Ryukyu Islands, where, for example, place-names of the type Pira correlate with Ainu pira
“rock” (Kagami 1962; Beleňkaja 1964). There are surprising biological similarities between
Ainu and the Ryukyans, especially visible on new-born children (Levin 1971, 197; Hudson
1994, 247), supported by evidence of molecular genetics (Cavalli-Sforza et al. 1994, 232).
[Ed. History attests that a language in the Ainu language family was probably spoken in the Northern part of Honshu, the main Japanese island, until about 1000 CE, and modern Japanese people have a significant minority component of Ainu-like, Jomon-like ancestry arising from an admixture event ca. 1000 BCE with a Manchurian-like Yayoi population from Korea.]
There have been several attempts to solve the question of the genetic affiliation of the
Ainu language. Aside from some attempts at comparison which are rather romantic (with Hebrew [!] by Batchelor), or give quite unsystematic results, e.g. with Indo-European by Naert
(1958, 1961), Lindquist (1960) or Van Windekens (1961) — see critical reviews of Benveniste
(1960), Dolgopolsky (1963), Tailleur (1961), Refsing [ed.] (1998); or with ‘Palaeo-Eurasian’, i.e.
‘Caucasian’, Basque, Yenisseian, Burushaski, plus some Amerindian languages, by Tailleur
(1963, 1968), there are two main competing hypotheses:
(1) Altaic: first mentioned by Ramstedt; further defended e.g. by Street, Language 38[1962], 92–99; Patrie 1982 (critically reviewed e.g. by Helimski 1984); and more extensively in the ‘Euroasiatic’ concept including Altaic, Nivkh, Uralic, Indo-European etc.: Koppelmann1928, 1933; Ruhlen 1987, 131–32 and 1994, 16–20; Krippes, Ural-Altaische Jahrbücher 61 [1989],149–51; Greenberg 2000–2002;
(2) Austronesian and Austroasiatic (plus Thai-Kadai and Miao-Yao, together Austric): 1926, 1960; Sternberg 1929, 1933; Murayama 1992a, 1992b, 1993; Vovin 1993 (cf. thereview of Sidwell 1996).
Our research supports the Austric hypothesis. . . .
Ainu (and Nihali, in India) may represent peripheral remnants of this Austric macro-phylum (see Bengtson 1996, Blažek 1996). The following scheme depicts their mutual relations: In physical anthropology the Ainu type has generally been included in the Mongoloid subspecies. On the basis of DNA evidence, the genetic taxonomy of Cavalli-Sforza et al. (1988,6003; 1992, 5621; 1994, 231–32) postulates a ‘Northeast Asian’ branch, comprising the Ainu, Japanese, and Koreans, along with Tibetans, North Chinese, and others. Similar results were obtained by classical methods of physical anthropology (Alekseev & Trubnikova 1984, 88). On the other hand, some undoubtedly very archaic features, such as the Ainus’ profuse body hair, and characteristic Sundadont dentition, point to relations with Southeast Asia (Alekseev & Trubnikova 1984, 94–96; Turner 1989). We might also mention the remarkable closeness of gene frequencies between the Ainu people and the aborigines of Taiwan, for example IGKC,KM (1&1,2), P1(1) or RH, haplotype cDE (Cavalli-Sforza et al. 1994, 385–86, 425–26). The connection of the ancestors of the Ainu people with Southeast Asia was thoroughly argued by Sternberg (1929).
The earliest known presence of modern man in the Japanese archipelago is estimated at 30,000 years BP (e.g., Utanobori on Hokkaido, or Osinovka on Sakhalin: see Golubev & Lavrov1988, 206, 220). At 11.000 years BP the first ceramic artifacts appear (Cavalli-Sforza et al. 1994, 202, have this as early as 12.700 BP; in any case, it is the world’s first appearance of ceramics).The style of pottery changed ca. 10.000 BP, which is thought to indicate the advent of the Jômon culture (remarkably, on Sakhalin this technology was delayed by 2.000 years, comparedwith Hokkaido — see Golubev & Lavrov 1988, 225). The contemporary Ainu people are very probably the descendants of the creators of the Jômon culture (cf. Hudson 1994, 244; Cavalli-Sforza et al. 1994, 203, 232). About 400 BC a new population came to Kyushu from the Korean peninsula, the bearers of the culture called Yayoi. They brought a developed rice agriculture and an Altaic language (Proto-Japanese). The closest relative of Old Japanese was the language of the old Korean kingdom, Koguryŏ (cf. Hudson 1994, 246–47).
. . .
Conclusion
Following the great specialist in Austronesian (and African) languages, Otto Dempwolff, we assume that the preceding list of lexical parallels between Ainu and the Austric languages represents the first step in the inductive phase of the demonstration of genetic relationship (really a continuation of the first steps taken by Gjerdman, et al.). The following step (already begun, for example, by Norquest, 1998) consists of the formulation of regular phonetic correspondences, which should be verified during the deductive phase. We believe that future progress in comparative and historical Austric linguistics will lead to the complete demonstration of the membership of Ainu within the Austric macro-phylum (along with Austronesian, Thai-Kadai, Miao-Yao, Austroasiatic, and probably also Nihali). If our article helps to stimulate discussion of the position of Ainu in genetic classification, it has served its purpose.