Part of the lore of rigorous mathematics is that there are many relationships and patterns in mathematics that hold true numerically to many, many terms, but eventually fail.
The mathematician in me knows this but has never really seen it. The physicist in me assumes that anything that holds numerically to very high N will almost always hold forever even if you can rigorously prove that this is true.
John Carlos Baez at his Azimuth blog, however, has some doozies of the kinds of patterns that mathematicians lose sleep over and physicists wrongfully assume are universally true in his most recent post.
For example, describes a mathematical rule that holds for all numbers up to roughly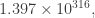 which is a very, very big number, even for physicists and economists. Ultimately, the rule is violated infinitely many times, oscillating between very large intervals where the rule works and very large intervals where the rule is always wrong.
which is a very, very big number, even for physicists and economists. Ultimately, the rule is violated infinitely many times, oscillating between very large intervals where the rule works and very large intervals where the rule is always wrong.
No comments:
Post a Comment