Most calculations in the Standard Model are made by adding up infinite series of Feynman diagrams to get a (complex valued) square root of a probability, called an amplitude. Each term in the series has an integer exponent of the coupling constant for the force whose effects are being evaluated which we call the number of "loops" in that diagram.
These calculations represent every possible way that a given outcome could happen, assign a (complex valued) amplitude to each such possibility, and add up the amplitudes of all possible ways that something could happen. This, in turn, gives us the overall probability that it will happen.
Since we can't actually calculate the entire series, we truncate it, usually at a certain number of "loops" which have the same coupling constant factor and represent the number of steps in virtual interactions that are involved in subsets of possible ways that the event we are considering could happen.
The trouble is that by truncating the series, we are implicitly assuming that the infinite number of remaining terms of the infinite series will collectively be smaller than the finite number of terms that we have already calculated. But, from a rigorous mathematical perspective, that isn't proper, because naively, these particular infinite series aren't convergent.
[T]he problem of the slow convergence of the infinite series path integrals we use do to QCD calculations isn't simply a case of not being able to throw enough computing power at it. The deeper problem is that the infinite series whose sum we truncate to quantitatively evaluate path integrals isn't convergent. After about five loops, using current methods, your relative error starts increasing rather than decreasing.
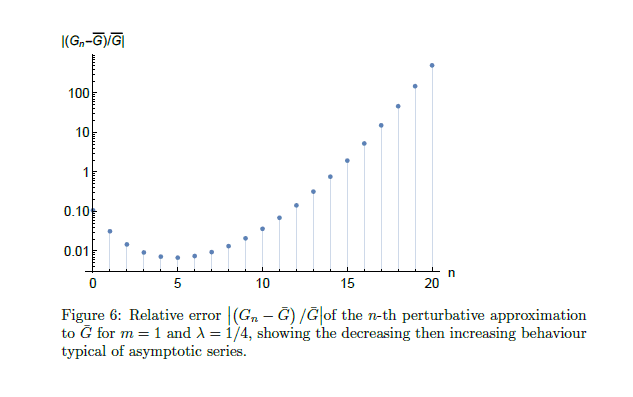
When you can get to parts per 61 billion accuracy at five loops as you can in QED, or even to the roughly one part per 10 million accuracy you can in weak force calculations to five loops, this is a tolerable inconvenience since our theoretical calculations still exceed our capacity to measure the phenomena that precisely [and the point of non-convergence also kicks in at more loops in these theories]. But when you can only get to parts per thousand accuracy at five loops as is the case in perturbative QCD calculations, an inability to get great precision by considering more loops is a huge problem when it comes to making progress.
Of course, despite the fact that mathematically, methods using non-convergent infinite series shouldn't work, in practice, when we truncate it, we do actually reproduce experimental results up to the expected precision we would get if it really were a convergent infinite series.
Nature keeps causing particles to behave with probabilities just in line with these calculations up to their calculated uncertainties.
So, for some reason, reality isn't being perfectly represented by the assumption that we have an infinite series with terms in powers of coupling constants, whose value at any given loop level is a probability that is not more than ± 1 (quantum mechanics employs negative probabilities in intermediate steps of its calculations).
There are at least two plausible reasons why this theoretically untenable approach works, they aren't mutually exclusive.
One is that the number of possible loops isn't actually infinite. Each step of an interaction represented by a Feynman diagram takes non-zero time. In these calculations, the probability calculated generally involves something happening at a finite distance. At some point, one has to discount the probability of having more than a given number of loops in a distance by the intrinsic limitation that there is a probability distribution of how long each step takes, and in the finite amount of time necessary to cover that finite distance, there needs to be an additional discounting factor, in addition to the coupling constant exponents themselves, at each subsequent loop, to reflect the probability that this many loops can be squeezed into a finite period of time.
There is a largely equivalent way of expressing this idea using an effective minimum length scale (perhaps the Planck length or perhaps even some larger value), rather than a probabilistic finite bound on the maximum number of loops that can impact a process that arises from related time and length limitations (either in isolation or when taken together).
A second is that there may be a "soft bound" on the contribution to the overall probability of an event that gets smaller at each subsequent loop, separate and apart from the coupling constant. This discount in the estimation of the error arising from the truncated terms would reflect the fact that at each Feynman diagram loop number, there are more and more individual Feynman diagrams that are aggregated, and that the amplitudes (the complex valued square roots of probability associated with each diagram) are pseudo-random. Thus, the more diagrams go into a given loop level calculation, the more likely they are to cancel out against each other, making probability distribution of the magnitude of the amplitude contributed to the total value at each subsequent loop have a strictly decreasing mean value at each successive greater number of loops. This means that the successive terms of the infinite series are getting smaller at a rate faster than we could rely upon, solely considering the exponent of the coupling constant at each loop.
In each of these cases, because reality seems to be convergent, even though the series naively isn't, this additional rate of diminution causes the additional terms in the series to get smaller at rate fast enough to make the series actually turn out to be a convergent infinite series once we understand its structure better. It could be that either of these considerations in isolation, which are largely independent of each other, is sufficient to produce this result, or it could be that you need both of these adjustment to reach the convergence threshold.
I'm sure that I haven't exhausted the entire realm of possibilities. It may be that one can limit oneself to on shell terms only or some other way out ignoring certain terms, and beat the convergence problem. Or, as I noted previously:
It might be possible to use math tricks to do better. For example, mathematically speaking, one can resort to techniques along the lines of a Borel transformation to convert a divergent series into a convergent one. And, path integral formulations are limitations associated with perturbative QCD calculations that can be overcome by using non-perturbative QCD methods like lattice QCD.
Nonetheless, it seems likely that including one or both of these factors that make the infinite series terms get smaller faster than we usually mathematically assume that they must when we make only weaker assumptions about the values of the terms that are multiplied by the coupling constant power scale factor at each loop, could be part of the solution.
It likewise must surely be the case that a "correct" description of reality does not dependent upon a quantity that is truly correctly calculated by adding up the terms of an unmodified non-convergent infinite series. Either these solutions, or something along the lines of these considerations, must be present in a "correct" formula that can perfectly reproduces reality (at least in principle).
No comments:
Post a Comment