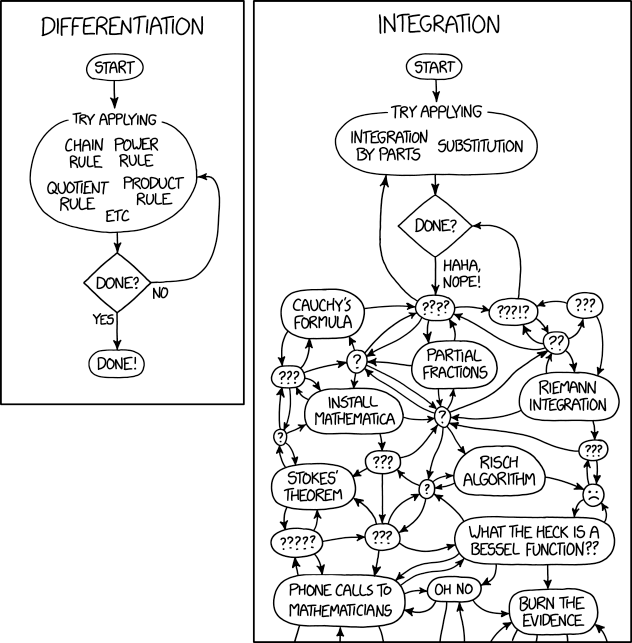
Alt Text: "Symbolic Integration" is when you theatrically go through the motions of finding integrals, but the actual result you get doesn't matter because it's purely symbolic."
("Symbolic integration" actually means solving an integral analytically in a general indefinite integral form, rather than numerically.)
A procedure called the Risch algorithm exists which is capable of determining whether the integral of an elementary function (function built from a finite number of exponentials, logarithms, constants, and nth roots through composition and combinations using the four elementary operations) is elementary and returning it if it is. In its original form, Risch algorithm was not suitable for a direct implementation, and its complete implementation took a long time. It was first implemented in Reduce in the case of purely transcendental functions; the case of purely algebraic functions was solved and implemented in Reduce by James H. Davenport; the general case was solved and implemented in Axiom by Manuel Bronstein.
However, the Risch algorithm applies only to indefinite integrals and most of the integrals of interest to physicists, theoretical chemists and engineers, are definite integrals often related to Laplace transforms, Fourier transforms and Mellin transforms. Lacking of a general algorithm, the developers of computer algebra systems, have implemented heuristics based on pattern-matching and the exploitation of special functions, in particular the incomplete gamma function.[1] Although this approach is heuristic rather than algorithmic, it is nonetheless an effective method for solving many definite integrals encountered by practical engineering applications. Earlier systems such as Macsyma had a few definite integrals related to special functions within a look-up table. However this particular method, involving differentiation of special functions with respect to its parameters, variable transformation, pattern matching and other manipulations, was pioneered by developers of the Maple[2] system then later emulated by Mathematica, Axiom, MuPAD and other systems.
The fact that a function in calculus and its inverse are profoundly different in difficulty is very non-intuitive but is definitely true. The assumption that they should be similar in difficulty is similar to the faulty reasoning behind "naturalness" as a hypothesis generator and evaluator in physics.
The "alt text" while seemingly just tongue in cheek word play actually hints at a deeper truth as well. While "symbolic integration" doesn't mean what the alt text says that it does, it isn't actually uncommon in theoretical physics to have a paper that calculates something as a proof of concept or a demonstration of a method when the actual result of the calculation doesn't matter.
FYI: This blog is currently one post short of its 3% humor quota.
No comments:
Post a Comment